Вероятностное описание случайной погрешности

 

Пусть произведено измерение некоторой величины х. Обозначим результат изме­рения x_изм. Абсолютная погрешность измерения равна

Dx = x_изм – x.

Погрешность Dx является случайной величиной и может быть представлена в виде суммы математического ожидания m_Dx и центрированной случайной величины :

.

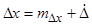Неслучайную составляющую m_Dx называют систематической погрешностью, а центрированную случайную величину - случайной погрешностью.

Если систематическая погрешность m_Dx известна, то результат измерения можно исправить, введя поправку:

х_испр = х_изм - m_Dx.

Аналогично исправить случайную погрешность не представляется возможным, так как конкретное значение этой погрешности в каждом измерении неизвест­но. Случайная погрешность может быть проанализирована вероятностными методами. Влияние случайной погрешности на результат измерения может быть оценено следующим образом. Задаются некоторыми предельными значениями погрешностей D₁ и D₂ и находят вероятность того, что измеряемая величина находится в интервале [ х_изм -D₁ ; х_изм + D₂]. Этот интервал называется доверительным , а вероятность того, что измеряемая величина находится внутри этого интервала – доверительной вероятностью Р_Д.

В том случае, когда случайная погрешность распределена по нормальному закону часто доверительный интервал представляют в симметричной форме:

 

где z=D/s, Ф(z₁) – интеграл вероятности, обычно определяемый по таблицам. На рис. 7.3. показана зависимость интеграла вероятности от соотношения между текущей погрешностью D и ее средним квадратическим значением s. Погрешность, интеграл веро­ятности которой равен 0,5 называют вероятной погрешностью r. Для этой погрешности характерно то, что при повторных измерениях примерно в половине случаев фактическая погрешность будет меньше r, а в другой половине случаев – больше или равна r. Значение вероятной ошибки r=0,6745s. Из рис.7.3. видно, что по мере роста аргумента D/s интеграл вероятности быстро приближа­ется к единице. Другими словами, по мере расши­рения доверительного интервала вероят­ность того, что случайная погрешность не превысит этот интервал, быстро падает. Так, вероятность того, что погрешность измере­ния не превысит 2s, равна 0,954. То есть из тысячи измерений только в 46 случаях по­грешность превысит 2s. Аналогично, только в 3-х случаях погрешность превысит 3s. Такое событие можно считать весьма маловероятным. Доверительная погрешность, равная 3s, называется граничной. Если в ряду измерений встречают погрешность D>3s, то такое измерение полагают промахом и в дальнейшей обработке результатов измерений не учитывают. Этот критерий известен как “правило 3s“. В теории вероятностей и математической статистике находит применение также термин “а%-ный квантиль” – такая абсцисса функции распределения плотности вероятности, слева от которой находится а% площади под графиком этой функции. Другими словами, вероятность Р_а% того, что случайная погрешность D < D_а%, равна а% . Интерквантильным промежутком называют разность между а%-ным и (100 - а)%-ным квантилями.

Нормальное распределение является часто встречающимся, но единственным в метрологии и измерительной технике. Находят также равномерное распределение:

По этому закону распределяются погрешности от трения в опорах стрелочных приборов, погрешности округления, погрешности отсчета результата по шкале прибора. Дисперсия равномерного распределения равна а²/12.

Треугольный закон распределения:

По преугольному закону распределяется сумма двух случайных величин, каждая из которых распределена равномерно.