Параграф 2.4.2.1: Импульсная характеристика, интеграл Дюамеля, дифференциальные уравнения системы.

Наиболее распространенной временной характеристикой (т.е. описывающей свойства системы во временной области) линейных систем является импульсная характеристика h(t) (реакция).

Импульсной характеристикой называется сигнал на выходе системы, при воздействии на ее вход единичного импульса, описываемого δ функцией:

Очевидно, что импульсная характеристика, так же как и порождающая ее δ функция, есть математическая абстракция. Физически она может быть оценена при подаче на вход импульсного сигнала единичной площади произвольной формы, длительность которого пренебрежимо мала по сравнению с характерным временным масштабом системы (например: периодом ее собственных колебаний, и постоянной времени). Зная импульсную реакцию минимальной стационарной системы можно определить ее отклик Uвых(t) на любой входное воздействие Uвх(t) с помощью интеграла свертки.

(*)

Это выражение обычно называется интегралом Дюамеля. Таким образом выходной сигнал линейной системы определяется как свертка входного сигнала и импульсной реакции. По виду импульсной реакции можно судить о физической реализуемости и устойчивости системы. По определению, для физически реализуемой системы необходимо выполнение условия.

h(t)=0, при t< 0.

Можно показать, что система будет устойчивой в том случае, когда импульсная реакция удовлетворяет условию:

Физический смысл условия заключается в том, при его выполнении h(t) представляет собой асимптотически убывающую функцию времени. Наряду с выражением (*), связь между выходными и входными сигналами линейной системы во временной области можно задать и по другому, с помощью следующего дифференциального уравнения:

(**)

Роль временной характеристики системы в данном случае выполняет набор коэффициентов a0, … , an, b0, … , bn, который для линейных стационарных систем представляет собой постоянные действительные числа. Если входной сигнал системы Uвх(t) задан в явном виде, то правая часть уравнения (**) является некоторой известной функцией f(t) и задача анализа системы сводится к решению дифференциального уравнения n-ого порядка с постоянными коэффициентами.

(***)

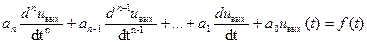Порядок n этого уравнения называют порядком системы. В уравнении (**) порядок тоже определяется значением n, поскольку для физически реализуемой системы необходимо выполнение условия . Из теории дифференциальных уравнений известно, что решением уравнения (***) является сумма некоторого частного решения неоднородного уравнения, у которого правая часть f(t) отлична от нуля и общего решения однородного уравнения

(****)

полученного из уравнения (***) путем замены в его правой части f(t) на 0. Общее решение уравнения (****) описывает собственные колебания линейной системы и имеет вид: 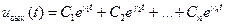, где — корни характеристического уравнения системы

(*****)

Эти корни могут быть как действительными, так и комплексными числами. Из формулы и (*****) видно, что если хотя бы один из корней будет иметь положительную действительную часть, то с ростом t U_вых(t) будет неограниченно возрастать. , и, следовательно, система будет неустойчивой. Т.о. условием устойчивости линейной системы заданы дифференциальным уравнением является отсутствие корней, характеризующих уравнения, имеющих положительную действительную часть (все корни должны быть расположены в левой части комплексной плюс-части). Если порядок системы достаточно высок, то нахождение корней характеристического уравнения может оказаться затруднительным, поэтому разработаны специальные критерии устойчивости, позволяющие определить наличие корней с положительной действительной частью непосредственно по значениям коэффициентов дифференциального уравнения без решения характеристического уравнения.