Контактно – гидродинамическая теория смазки

Теорию контактно – гидродинамической смазки можно кратко определить как науку об изучении условий, в которых упругая деформация контактирующих тел играет существенную роль в гидродинамическом процессе смазки. В машиностроении много механизмов, где нагрузки передаются через сосредоточенные линейные или точечные контакты. Типичными примерами последних являются зубчатые передачи и подшипники качения.

Классическая гидродинамическая теория не позволяет объяснить, почему в самых жестких по уровню напряжений условиях должна существовать смазка, почему она способна противостоять таким давлениям. Однако если допустить зависимость вязкости от давления и упругую деформацию контактирующих твердых тел, то можно показать, что существует удовлетворительная смазка в таких условиях.

Рассмотрим схематично упругий линейный контакт (см. рис 13.5). Здесь мы наблюдаем возникновение клиновидного зазора. Течение смазки в таком зазоре описывается уравнением Рейнольдса

(13.1).

В таком контакте возникают огромные давления и вязкость меняет свою величину по приближенному закону Баруса: m =m₀ e^np, где m₀ – динамический коэффициент при атмосферном давлении, n – пьезокоэффициент вязкости смазки.

При действии гидродинамического давления происходит деформация поверхностей и меняется форма зазора между ними. Как известно, зазор между двумя круговыми цилиндрами до деформации на узком участке с большой точностью можно представить в виде квадратной параболы (рис.13.6)

Деформацию поверхности (прогиб) можно описать выражением

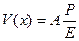, (13.2)

где А – коэффициент пропорциональности, Е – модуль упругости.

Форма зазора после деформации описывается уравнением

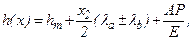(13.3)

где - приведенная кривизна контактирующих тел, x – координата точки, где определяется величина зазора.

Совместное решение уравнений (13.1) и (13.3) дает распределение толщины смазочного слоя и гидродинамического давления по площадке контакта, в виде представленном на рис 13.7. Контактно-гидродинамическая теория смазки позволила объяснить наличие смазочной пленки достаточной толщины при значительных давлениях в условиях сосредоточенного линейного и точечного контактов. Она позволяет подбирать такие режимы трения, при которых возникает жидкостное трение.