Метод простой итерации

Заменим уравнение F(x)=0 равносильным уравнением x = f(x).

Теорема.

Пусть уравнение x=f(x) имеет единственный корень на отрезке [a,b] и выполнены условия:

1) функция f(x) определена и дифференцируема на отрезке [a,b];

2) "x Î [a,b] f(x) Î [a,b]

3) $q "xÎ[a,b] |f’(x)|£q<1

Тогда итерационная последовательность x_n=f(x_n-1) (n=1,2,...) сходится при любом начальном члене x₀Î[a,b].

 

Таким образом, наша задача: преобразовать уравнение F(x)=0 к виду x = f(x), удовлетворяющему условиям теоремы 1-3 (хотя итерационная последовательность может сходиться и при невыполнении некоторых условий).

В зависимости от вида функции сходимость может происходить ступеньками либо по спирали.
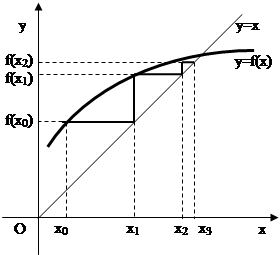