Законы сохранения и их связь со свойствами однородности времени, однородности и изотропии пространства.

Способность уравнения, описывающего физический процесс, сохранять свою форму при некотором преобразовании называется симметрией или инвариантностью относительно этого преобразования. Сохранение формы записи уравнения в разных системах координат означает, что физический процесс развивается одинаковым образом в этих системах координат. В современной физике понятия симметрии или инвариантности играют фундаментальную роль. Из принципа симметрии всегда следует закон сохранения.

Опыт механики, накопленный за всю историю ее развития, указывает на то, что движение замкнутой системы не изменяется, если все движущиеся тела одновременно переместить в пространстве на один и тот же вектор. Это свойство называют однородностью пространства.

Другой вид симметрии связан с тем, что свойства замкнутой системы не изменяются, если повернуть систему как целое вокруг некоторой оси на произвольный угол. Т.е. все направления в пространстве равноценны. Это свойство называется изотропией пространства.

Еще один вид симметрии – однородность законов движения по отношению к переносам во времени. Т.е. все моменты времени равноправны и любой момент времени можно принять за начало отсчета. Это свойство называется однородностью времени.

1) Закон сохранения энергии следует из свойства однородности времени.

В силу однородности времени функция Лагранжа не будет явно зависеть от времени: 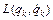, т.е. должно быть: . (1)

Запишем полную производную функции Лагранжа по времени. 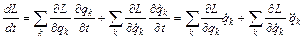(2)

Заменим в (2) производные 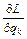, используя уравнение Лагранжа 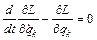. (3)

Тогда (2) с учетом (3) :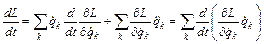или

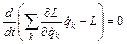
величина 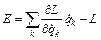(4)

сохраняется и называется обобщенной энергией системы. (4) является самым общим выражением энергии произвольной системы и остается пригодным при описании не только энергии механических систем, но и энергии полей.

2) Закон сохранения импульса следует из свойства однородности пространства.

Выберем систему из N тел без связей и запишем функцию Лагранжа для этой системы в декартовых координатах:

, k =1,..., N. (5)

Рассмотрим перенос всех тел системы в направлении вектора 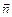на бесконечно малое расстояние e. (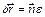). В силу однородности пространства изменение функции Лагранжа при таком переносе должно быть равно нулю:

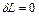. (6)

Изменение функции Лагранжа в результате малого изменения координат при неизменных скоростях тел системы будет равно:

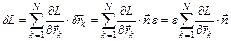. (7)

В силу произвольного выбора чтобы выполнялось условие (6) следует предположить, что 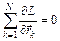. (8)

Используя уравнение Лагранжа (3), перепишем (8) в виде:

.

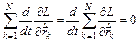Отсюда следует, что величина 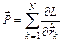будет постоянной при перемещении системы. Вектор 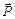называется импульсом системы. Дифференцируя функцию Лагранжа (5), получим, что

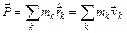
Как видно из последнего соотношения, импульс системы является аддитивной величиной, т.е. импульс системы равен сумме импульсов тел.

3) Закон сохранения момента импульса следует из свойства изотропии пространства.

Рассмотрим поворот системы как целого на малый угол dj = e относительно оси, направление которой задается единичным вектором 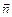по правилу правого винта. Введем вектор . Выберем начало координат в какой-нибудь точке на оси поворота. При повороте на угол dj произвольный 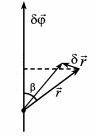радиус-вектор 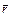получит приращение, которое запишется следующим образом: 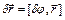. (9)

При повороте системы меняется не только направление радиус-векторов, но и направления скоростей материальных точек. При этом все векторы преобразуются по одинаковому закону. Т.е. приращение скорости при повороте будет происходить по правилу:

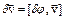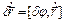или (10)

В силу изотропии пространства при поворотах функция Лагранжа не изменяется:

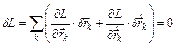(11)

Используем в (11) соотношения (9) и (10) и учтем, что 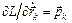, , 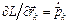тогда (11) примет вид:

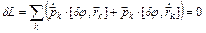(12)

Выполним в (12) циклическую перестановку множителей и вынесем dj за знак суммы:

Т.к. dj было выбрано произвольно, то отсюда следует, что 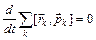. Т.е. при повороте системы как целого сохраняется векторная величина , которая называется моментом импульса системы. – моменты импульса отдельных тел.