Искусственные нейронные сети.

ИНС – вид математических моделей, которые строятся по принципу организации и функционирования их биологических аналогов – сетей нервных клеток мозга. В основе их построения лежит идея о том, что нейроны можно моделировать довольно простыми автоматами, называемыми искусственными нейронами, а вся сложность мозга, гибкость его функционирования и другие важнейшие качества определяются связями между нейронами.

История ИНС начинается с 40- годов 20 века, когда двое американских исследователей – У. Маккалок и У. Питтс – предложили модель нейрона и сформулировали основные положения теории функционирования человеческого мозга.

Существует множество задач, для решения которых может быть использован аппарат искусственных нейронных сетей.

Рассмотрим в качестве примера задачу распознавания образов. Пусть имеется некоторое изображение. Необходимо определить, что на нем изображено и где. Если написать программу, решающую данную задачу, придется последовательно, перебирая отдельные пиксели изображения в соответствии с некоторым критерием, решить, какие из них принадлежат определенному объекту. Сформулировать критерий, определяющий конкретный выбранный объект, является нетривиальной задачей.

На этом примере можно сформулировать несколько принципиальных отличий в обработке информации в мозге и в ЭВМ:

1. Способность к обучению на примерах.

2. Способность к обобщению, то есть мы не просто запомнили все примеры некоторого объекта, но и создали некоторый идеальный образ абстрактного объекта. Сравнивая с ним множество других объектов, можно определить, похож он на него или нет.

3. Параллельность обработки информации. Данное отличие означает, что картинка не считывается по пикселям, мы видим ее целиком и наш мозг целиком ее обрабатывает.

4. Надежность.

5. Ассоциативность памяти – способность находить нужную информацию по ее малой части.

Мозг человека состоит из нервных клеток – нейронов. Всего их 10¹² штук. Каждый нейрон мозга имеет один длинный ветвящийся отросток – аксон и множество мелких ветвящихся отростков – дендритов.

Известно, что в ответ на возбуждение нейрон может генерировать нервный импульс, распространяющийся вдоль аксона, то есть это волна деполяризации мембраны нейрона. Она является автоволной, то есть ее форма и скорость распространения не зависят от того, как и из-за чего она возникла.

Доходя до конца аксона, волна вызывает выделение веществ, называемых нейромедиаторами. Воздействуя на дендриты других нейронов, они могут, в свою очередь, вызвать появление в них нервных импульсов.

Когда суммарный сигнал, приходящий от других нейронов, превышает некоторое пороговое значение, генерируется стандартный импульс. В противном случае нейрон остается в состоянии покоя.

Биологический нейрон – сложная система, математическая модель которой до конца не построена. В основе теории искусственных нейронных сетей лежит предположение о том, что вся эта сложность несущественна, а свойства мозга объясняются характером их соединения.

Поэтому вместо точных математических моделей нейронов используется простая модель так называемого формального нейрона. Он имеет входы, куда подаются некоторые числа: x1, …, xn. Затем стоит блок, называемый адаптивным сумматором. На его выходе мы имеем взвешенную схему входов: S=S_n ⁱ⁼¹x_i*w_i. Затем она подается на нелинейный преобразователь и на выходе мы имеем y=F(S).

Слева – адаптивный сумматор, справа – нелинейный преобразователь.

Функция F нелинейного преобразователя называется активационной функцией нейрона. Исторически первой была модель, в которой в качестве активационной функции использовалась ступенчатая функция, или функция единичного скачка.

F(S)={ 0, S<0

1, S>=0}

По аналогии с биологическим нейроном, когда суммарное воздействие на входе превысит критическое значение, генерируется импульс 1. Иначе нейрон остается в состоянии покоя, то есть выдается ноль.

Существует множество других функции активации. Одной из наиболее распространенных является логистическая функция (сигмоид), которая описывается следующим образом:

f(x)=1/1+e^{-альфа х}

При уменьшении альфа сигмоид становится более пологим, в пределе при альфа=0 вырождаясь в горизонтальную линию. При увеличении альфа сигмоид приближается по внешнему виду к функции единичного скачка с порогом в точке х=0.

Архитектуры нейронных сетей.

Выделяют несколько стандартных архитектур, из которых путем вырезания лишнего или добавления строят большинство используемых сетей. Можно выделить две базовые архитектуры: полносвязные и многослойные сети.

В полносвязных нейронных сетях каждый нейрон передает свой выходной сигнал остальным нейронам, в том числе и самому себе. Все входные сигналы подаются всем нейронам. Выходными сигналами сети могут быть все или некоторые выходные сигналы нейронов после нескольких тактов функционирования сети.

В многослойных нейронных сетях (их часто называют персептронами) нейроны объединяются в слои. Слой содержит совокупность нейронов с едиными входными сигналами. Число нейронов в слое может быть любым и не зависит от количества нейронов в других слоях.

В общем случае сеть состоит из нескольких слоев, пронумерованных слева направо. Внешние входные сигналы подаются на входе нейронов входного слоя (его часто нумеруют как нулевой), а выходами сети являются выходные сигналы последнего слоя. Кроме входного и выходного слоев, в многослойной нейронной сети есть один или несколько так называемых скрытых слоев.

В свою очередь, среди многослойных сетей выделяют:

1. Сети прямого распространения – сети без обратных связей. В таких сетях нейроны входного слоя получают входные сигналы, преобразуют их и передают нейронам первого скрытого слоя, и так далее вплоть до выходного, который выдает сигналы для интерпретатора и пользователя.

Если не оговорено противное, то каждый выходной сигнал n-ного слоя передастся на вход всех нейронов n+1 слоя.

Рисунок – Многослойная (трехслойная) сеть прямого распространения.

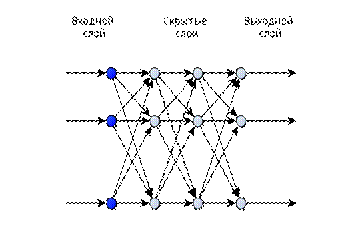
2. Сети с обратными связями (рекуррентные сети). В таких сетях информация передается с последующих слоев на предыдущие. Следует иметь в виду, что после введения обратных связей сеть уже не просто осуществляет отображение множества входных векторов на множество выходных, она превращается в динамическую систему и возникает вопрос об ее устойчивости.

Теоретически число слоев и число нейронов в каждом слое может быть произвольным. Однако фактически оно ограничивается ресурсами ЭВМ, на которой реализуется нейросеть.

Чем сложнее сеть, тем более сложные задачи она может решать. Рассмотрим более подробно свойства многослойных нейронных сетей прямого распространения. Рассмотрим также задачи, которые может решать подобная нейросеть:

1. Задача классификации. Рассмотрим более подробно, что делает один формальный нейрон в самом простом случае, когда его функцией активации является ступенька. Он дает на выходе 1, если выполняется условие:

S=Sⁿ _i-1wi*xi+w0 >=0

И выдает 0, если S<0. Таким образом он разбивает пространство входов на две части с помощью некоторой гиперплоскости. Если у нас всего два входа, то это пространство двухмерно и нейрон будет разбивать его с помощью прямой линии.

Это разбиение определяется весовыми коэффициентами wi нейрона. Если мы составим из N таких нейронов слой, то получим разбиение пространства входов N гиперплоскостями. Каждой области в этом пространстве будет соответствовать некий набор нулей и единиц, формирующийся на выходе нашего слоя.

Таким образом, такая нейронная сеть пригодна для решения задачи многомерной классификации или распознавания образов. Допустим, у нас есть некий объект, имеющий набор свойств x1, x2, .., xn. Мы можем подать эти параметры на вход сети и сказать, что определенная комбинация нулей и единиц на выходе соответствует определенному объекту.

Таким образом, наша сеть способна выполнять операцию распознавания. Очевидно, что не для всякой задачи распознавания существует однослойная сеть, ее решающая. Идеальным случаем является случай, когда распределение точек в пространстве параметров такое, когда достаточно провести одну линию (или гиперплоскость), чтобы разделить эти два множества. В этом случае достаточно одного нейрона.

В более общем случае такое невозможно. Тогда используется слой нейронов, но одному множеству будет соответствовать уже не одна, а множество комбинаций нулей и единиц. Если выходы первого слоя нейронов используются в качестве входов для нейронов второго слоя, то нетрудно убедиться, что каждая комбинация нулей и единиц на выходе второго слоя может соответствовать некоему объединению, пересечению и инверсии областей, на которое пространство входов разбивалось первым слоем нейронов.

Двухслойная сеть, таким образом, может выделять в пространстве входов произвольные выпуклые односвязные области. В случае еще более сложной задачи, когда требуется различать многосвязные области произвольной формы, всегда достаточно трехслойной сети.

2. Задача аппроксимации функций. Рассмотрим сеть, нейроны которой в качестве функции активации имеют не ступеньку, а некоторую непрерывную функцию, например, сигмоид. В этом случае выход сети будет некоторой непрерывной функцией ее входов. Конкретный вид этой функции определяется весовыми коэффициентами каждого из нейронов.

Возникает вопрос, какие функции могут быть аппроксимированы с помощью нейронной сети. Ответ на этот вопрос дает обобщенная теорема Стоуна. Ее можно интерпретировать как утверждение об универсальных аппроксимационных возможностях произвольной нелинейности: с помощью линейных операций и каскадного соединения можно из произвольного нелинейного элемента получить устройство, вычисляющее любую непрерывную функцию с любой наперед заданной точностью.

То есть нейросеть с произвольной функцией активации может аппроксимировать произвольную непрерывную функцию. При этом, как оказывается, всегда достаточно трехслойной сети. Вопрос повышения точности решается добавлением нейронов в сеть.

Как частный случай задачи аппроксимации можно рассмотреть задачу предсказания временных рядов. На вход подается некоторое количество предыдущих значений, а на выходе получаются значения в следующий момент времени.

При решении различных задач с помощью аппарата искусственных нейронных сетей возникает вопрос, как подобрать такие весовые коэффициенты, чтобы сеть решала задачу распознавания или аппроксимировала некоторую функцию.

Одним из главных свойств нейронных сетей является то, что их этому можно научить. Алгоритмы обучения бывают трех видов:

1. Обучение с учителем. При этом сети предъявляется набор обучающих примеров. Каждый обучающий пример представляет собой пару: вектор входных значений и делаемый выход сети. Например, для обучения предсказанию временных рядов это может быть набор нескольких последовательных значений ряда и известное значение в следующий момент времени.

В ходе обучения весовые коэффициенты подбираются таким образом, чтобы по этим входам давать выходы, максимально близкие к правильным.

2. Обучение с поощрением. При этом сети не указывается точное значение желаемого выхода, но ей выставляется оценка, хорошо она поработала или плохо.

3. Обучение без учителя. В этом случае предъявляются некоторые входные векторы и в ходе их обработки в ней происходят некоторые процессы самоорганизации, приводящие к тому, что сеть становится способной решать какую-то задачу.

Рассмотрим один из самых популярных алгоритмов обучения – так называемый алгоритм обратного распространения. Это один из вариантов обучения с учителем.

Пусть у нас имеется многослойная сеть прямого распространения со случайными весовыми коэффициентами. Есть некоторое обучающее множество, состоящее из пар: вход сети – желаемый выход: {X, D}. Через Y обозначим реальное выходное значение нашей сети, которое вначале практически случайно из-за случайности весовых коэффициентов.

Обучение состоит в том, чтобы подобрать весовые коэффициенты таким образом, чтобы минимизировать некоторую целевую функцию. В качестве целевой функции рассмотрим сумму квадратов ошибок сети на примерах из обучающего множества: E(w)= S_{j p} (yⁿ _j,p- d _j,p )², где: (1)

yⁿ _{j,p -} реальный выход n-ного выходного слоя сети для p-того нейрона на j-том обучающем примере,

d _j,p - желаемый выход.

То есть минимизировав такой функционал, мы получим решение по методу наименьших квадратов.

Поскольку весовые коэффициенты в зависимость y^(N)_j,p(х) входят нелинейно, воспользуемся для нахождения минимума методом наискорейшего спуска. То есть на каждом шаге обучения будем изменять весовые коэффициенты по формуле:

Дельта w⁽ⁿ⁾_ij= - η * dE/d w⁽ⁿ⁾_ij, где (3)

w⁽ⁿ⁾_ij – весовой коэффициент j-того нейрона n-ного слоя для связи с i-тым нейроном n-1-ого слоя. Параметра η называется параметром скорости обучения.

Таким образом, требуется определить частные производные весовой функции E по всем весовым коэффициентам сети. Согласно правилам дифференцирования сложной функции получим:

Формулу 3

Где

yⁿ_j - выход

zⁿ_{j –} взвешенная сумма входов j-того нейрона n-ного слоя.

Зная функцию активации, можно вычислить формулу 4.

Например, для сигмоида эта величина будет равняться: херня 5.

Третий сомножитель в формуле 3 есть не что иное, как выход i-того нейрона n-1-ого слоя. То есть:

херня 6 с номером 5

ϪѠ

Частные производные целевой функции по весам нейронов выходного слоя теперь можно легко вычислить.

Производя дифференцирование 1 по херне 7 и учитывая выражения 3 и 5, получим херня 8 с номером 6.

Введем обозначения:

Херня 9 с номером 7

Тогда для нейрона выходного слоя получим:

Херня 10 с номером 8

Окончательную формулу 2 для модификации весовых коэффициентов можно записать в виде:

Херня 11 с номером 9

Таким образом, полный алгоритм обучения нейронной сети с помощью алгоритм обратного распространения строится следующим образом:

1. Присваиваем всем весовым коэффициентам сети случайные начальные значения. При этом сеть будет осуществлять какое-то случайное преобразование входных сигналов и значения целевой функции 1 будут велики.

2. Подать на вход сети один из входных векторов из обучающего множества. Вычислить выходные значения сети, запоминая при этом выходные значения каждого из нейронов.

3. Рассчитать значение величины херня 12, затем рекурсивно подсчитываются все остальные значения херня 13 и с помощью формулы 9 изменение весовых коэффициентов сети.

4. Скорректировать веса сети: херня 14.

5. Рассчитать целевую функцию, используя выражение 1. Если она достаточно мала, считать сеть успешно обучившейся. Иначе возвращаемся на шаг 2.

Основные проблемы, возникающие при применении данного метода:

1) Локальные минимумы. Алгоритм обратного распространения реализуется градиентный спуск по поверхности ошибки в пространстве весовых коэффициентов и поэтому может застревать в локальных минимумах. При этом рядом может иметься другой, значительно более глубокий минимум.

Для преодоления этой проблемы обучение сети проводят несколько раз и затем выбирают тот вариант обученной сети, который дает наилучшие результаты. Другой метод заключается в том, что сеть можно вывести из локального минимума на короткое время, увеличив скорость обучения.

Иногда к изменению весовых коэффициентов, вычисленному по алгоритму, добавляют шум. Это также позволяет сети «выпрыгивать» из локальных минимумов.

2) Паралич сети. В процесс обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших аргументах функции активации херня 15 в области, где произвольная функции крайне мала, как например, для сигмоидной функции активации.

Так как величина коррекции весов пропорциональна этой производной, то процесс обучения может практически замереть. Для преодоления такой ситуации существуют модификации алгоритма, учитывающие лишь направление антиградиента и не учитывающие его величину.