Частотный критерий Михайлова
Этот критерий был сформулирован и обоснован А.В. Михайловым в 1936 г. и послужил началом широкого применения частотных методов в теории автоматического управления.
Он также основан на анализе характеристического уравнения системы. Левую часть характеристического уравнения системы называют характеристическим полиномом, который имеет вид
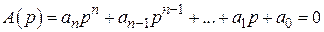. (7.13)
Если в (7.13) подставить вместо переменного р чисто мнимый корень р = jw, то получим функцию комплексного переменного
, (7.14)
которую можно так же, как и амплитудно-фазовую характеристику, представить в виде суммы действительной и мнимой частей (вектор Михайлова):
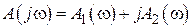. (7.15)
Действительная часть А1(w) содержит только четные степени переменной частоты ω
, (7.16)
а минимальная часть А2(ω) – только нечетные:
. (7.17)
Каждому фиксированному значению частоты соответствует комплексное число, которое можно изобразить в виде вектора на комплексной плоскости.
Если изменять частоту ω от 0 до +∞, то конец вектора Михайлова в комплексной плоскости (А1, jA2) будет поворачиваться, изменяя свою длину, и опишет кривую, которую называют годографом Михайлова (или годографом вектора характеристической функции). По виду этой кривой можно судить об устойчивости системы.
| Формулировка критерия Михайлова: система автоматического регулирования будет устойчивой, если при изменении частоты от нуля до бесконечности годограф Михайлова обходит последовательно в положительном направлении (т.е. против часовой стрелки) n квадрантов комплексной плоскости, где n – степень характеристического уравнения системы (рис. 7.5). |
| Рис. 7.5 Годографы Михайлова для систем n=1,2,3,4,5 – порядков. I,II,III,IV и т.д. – номера квадрантов комплексной плос-кости. Системы устойчивы |
Из выражений (7.16) и (7.17) следует, что годограф Михайлова всегда начинается в точке на действительной оси, удаленной от начала координат на величину а0.
Характеристические кривые (годограф Михайлова), соответствующие устойчивым системам (рис. 7.5), имеют спиралевидную форму и уходят в бесконечность в том квадранте, номер которого равен порядку характеристического уравнения.
| Рис. 7.6. Годографы Михайлова: 1 – система устойчива; 2 – система неустойчива; 3 – система на границе устойчивости |
Если годограф Михайлова проходит n квадрантов не последовательно (последовательность квадрантов нарушается) или проходит меньшее число квадрантов, то система неустойчива (рис. 7.6).
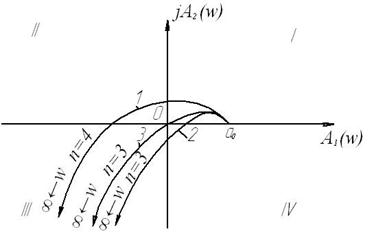
Если годограф проходит через начало координат, то система находится на границе устойчивости (рис. 7.6).
В практических расчетах удобно применять следствие из критерия Михайлова: система автоматического регулирования устойчива, если действительная и мнимая части вектора характеристической функции (вектора Михайлова) обращаются в нуль поочередно, т.е., если корни уравнений
А1(ω) = 0 и А2(ω) = 0 (7.18)
перемежаются.
Это утверждение следует непосредственно из формулировки критерия Михайлова – из условия последовательного прохождения годографа Михайлова (годографа вектора характеристической функции) через n квадрантов.
Критерий Михайлова удобно применять для анализа устойчивости систем высокого порядка (n>5).