Алгебраический критериЙ устойчивости Гурвица

Критерий основан на построении определителя, составленного из коэффициентов, входящих в характеристическое уравнение системы.

Запишем характеристическое уравнение для системы 6-го порядка в виде

. (7.11)

Аналогично можно записать уравнение системы любой степени, если порядок системы обозначить n. В нашем случае n=6.Уравнение записывается таким образом, чтобы коэффициент при высшей производной (а₆) был положительным, т.е. а₆ > 0.

Порядок построения определителя Гурвица.

1. По главной диагонали записываются все коэффициенты от до а₀ включительно (=5).

2. Вверх по диагонали записываются коэффициенты уравнения в порядке убывания индексов, а вниз от диагонали – в порядке возрастания индексов.

3. На месте коэффициентов, не входящих в характеристическое уравнение, ставят нули.

4. Определители меньших порядков получают вычеркиванием последнего столбца и последней строки.

5. Определитель высшего порядка D_n=a₀D_n-1 (D₆=а₀D₅).

Условие устойчивости по Гурвицу

Система автоматического управления будет устойчивой, если все определители, составленные из коэффициентов характеристического уравнения системы, от D_n (D₆) до D₁ будут положительными, при этом а_n (а₆) должно быть больше нуля.

Построим определитель Гурвица для системы шестого порядка.

.

Система устойчива, если а₀>0; D₅>0; D₄>0; D₃>0; D₂>0; D₁=а₅>0.

Если хотя бы один из определителей, называемых определителями Гурвица, отрицателен, система будет неустойчива.

 

Если главный определитель системы D_п=0, а все остальные определители положительны, то система находится на границе устойчивости.

Рассмотрим частные случаи критерия Гурвица для систем 1, 2, 3-го порядков. Раскрывая определители, фигурирующие в общей формулировке критерия, можно получить следующие условия.

1. Для уравнений первого порядка

,

условие устойчивости

а₁ > 0 и D₁ = а₀ > 0,

т.е. необходимым и достаточным условием устойчивости является положительность коэффициентов уравнения (<0).

2. Для уравнений второго порядка

,

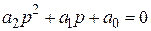условие устойчивости

а₂ > 0, D₁ = а₁ > 0; D₂ = а₀а₁ > 0.

Таким образом, и для системы второго порядка положительность коэффициентов является необходимым и достаточным условием устойчивости.

3. Для уравнений третьего порядка

,

условие устойчивости

а₃ > 0, D₁ = а₂ > 0; D₂ = а₁а₂ – а₀а₃ > 0; D₃ = а₀D₂ > 0.

Последнее неравенство Δ₃ > 0 эквивалентно неравенству D₂ > 0. Следовательно, для системы третьего порядка кроме положительности всех коэффициентов уравнения требуется, чтобы D₂ > 0.

Критерий Гурвица применяют для анализа устойчивости систем не выше пятого порядка. При n > 5 вычисление определителей становится громоздким.