Тема 13. Игры в условиях риска

В рассмотренных антагонистических играх присутствовала неопределенность, состоящая в том, что ни один из игроков не обладал информацией о действиях противника. Тем не менее эта неопределенность в некоторой степени компенсировалась определенным предположением каждого из игроков о том, что противоборствующая сторона действует осознанно, выбирая стратегии, наиболее выгодные для себя и наименее выгодные для противника, т. е. поведение каждого игрока было нацелено на увеличение своего выигрыша (уменьшение проигрыша).

Однако, в экономической практике во многих задачах принятия решений существенно важным элементом является неопределенность иного вида, не связанная с сознательным целенаправленным противодействием противника и заключающаяся в недостаточной информированности лица, принимающего решение, об объективных условиях, в которых будет приниматься решение. Неопределенность такого рода может порождаться различными причинами: нестабильность экономической ситуации, покупательский спрос на товар конкретного вида, меняющийся объем перевозок, рыночная конъюнктура, политика правительства, надежность партнера, выход из строя технического оборудования, курс валюты, уровень инфляции, налоговая политика, биржевая ситуация, экологическая обстановка, стихийные бедствия и др.

Во всех задачах такого рода выбор решения зависит от объективной действительности, называемой в математической модели "природой". Сама же математическая модель подобных ситуаций называется "игрой с природой ".

Таким образом, в игре с природой осознанно действует только один игрок, а именно, лицо, принимающее решение; обозначим его через А. Природа, обозначим ее через П, является вторым игроком, но не противником игрока А, ибо она не действует осознанно против игрока А, а принимает неопределенным образом то или иное свое состояние, не преследуя конкретной цели и безразлично к результату игры. Игрока А в игре с природой называют иногда статистиком, а теорию игр с природой - теорией статистических решений.

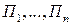Пусть игрок А имеет т возможных стратегий , а природа П может находиться в одном из п состояний , которые можно рассматривать как ее "стратегии".

Совокупность 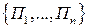формируется либо на основе имеющегося опыта анализа состояний природы, либо в результате предположений и интуиции экспертов. Выигрыш игрока А при выбранной им стратегии , и при состоянии 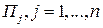, природы П обозначим . Так же, как и в матричной игре, из выигрышей игрока А можно сформировать матрицу выигрышей игрока А (матрицу игры, платежную матрицу)

 

			………
			………
………	………	……	………	………
			………

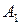
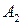
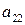
которая содержательно отличается от матрицы антагонистической игры тем, что элементы столбцов не являются проигрышами природы при соответствующих ее состояниях.

Задача выбора игроком А чистой или смешанной стратегии, более эффективной, чем остальные, в игре с природой, с одной стороны, проще аналогичной задачи в антагонистической игре, поскольку в игре с природой отсутствует с ее стороны систематическое противодействие игроку А, а с другой стороны, эта задача осложняется наличием неопределенности, связанной с дефицитом осведомленности игрока А о характере проявления состояний природы.

Если какая-нибудь из стратегий игрока А окажется доминирующей каждую из остальных его стратегий, то она и должна выбираться игроком А в качестве предпочтительной, поскольку его выигрыш при этой стратегии и при любом состоянии природы П не меньше выигрыша при любой из остальных стратегий.

Например, в игре с природой с матрицей

При решении вопроса о выборе возможной стратегии в игре с природой игрок А должен исходить из матрицы выигрышей. Однако матрица выигрышей не всегда адекватно отражает имеющуюся ситуацию. На выбор стратегии должны влиять не только выигрыши, составляющие матрицу игры, но и показатели "удачности" или "неудачности" выбора данной стратегии при данном состоянии природы и благоприятности этого состояния для увеличения выигрыша.

Показателем благоприятности состояния природы П для увеличения выигрыша называется наибольший выигрыш при этом состоянии, т. е. наибольший элемент 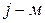столбце матрицы игры:

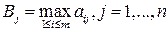. (13.1)

Таким образом, благоприятность состояния природы рассматривается как фактор, благоприятствующий увеличению выигрыша игрока А при этом состоянии природы.

В теории антагонистических матричных игр эта величина представляла собой показатель неэффективности стратегии игрока В

Для характеризации степени удачности применения игроком А стратегии, при состоянии природы П вводят понятие "риска".

Риском игрока А при выборе им стратегии в условиях состояния природы П называется разность между показателем благоприятности состояния природы и выигрышем , т. е. разность между выигрышем, который игрок А получил бы, если бы знал заранее, что природа примет состояние , и выигрышем, который он получит при этом же состоянии , выбрав стратегию т. е.

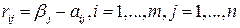(13.2)

Таким образом, риск игрока А при применении стратегиив условиях состояния природы есть упущенная им возможность максимального выигрыша при этом состоянии природы. Эта упущенная возможность определяется, как это следует из (13.2), невыигранной частью величины максимального выигрыша .

Из сказанного вытекает, что величину риска можно интерпретировать как своеобразную плату за отсутствие информации о состоянии природы.

Из формул (13.1) и (13.2) следует, что риск для любых инеотрицателен:

. (13.3)

Можно установить и верхнюю границу рисков для каждого состояния природы . Для этого введем в рассмотрение величину

(13.4)

представляющую собой наименьший выигрыш игрока А при состоянии природы . Тогда из (13.2)

(13.5)

Разность естественно назвать колебанием выигрышей при состоянии природы .

Если, то из (13.2) 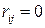, т. е. стратегия при состоянии природы является безрисковой.

Если 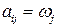, то риск , который по определению (13.2) равен , является максимальным (см. (13.5)). Следовательно, по критерию риска стратегия этом случае наихудшая.

Для матрицы А матрица рисков имеет ту же размерность и следующий вид:

=

			…
			…
			…
…	…	…	…	…
			…

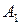
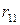
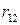
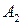
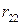
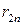
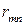
Отметим, что матрица выигрышей А однозначно порождает матрицу рисков , поскольку каждый риск однозначно определяется по формуле (13.2) соответствующими показателем благоприятности состояния природы и выигрышем . Обратное неверно: одна и та же матрица рисков может соответствовать разным матрицам выигрышей.

Пример 1. Рассмотрим игру с природой, для которой известна матрица игры

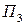
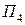
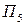
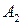
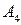
Необходимо построить матрицу рисков.

Дополним матрицу игры строкой показателей благоприятности состояний природы:

 

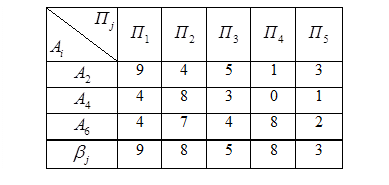(13.6)

Теперь вместо элемента в каждой ячейке первых трех строк матрицы (13.6) подставим разность между последним (четвертым) элементом столбца, в котором стоит заменяемый элемент, и заменяемым элементом; в результате получим матрицу рисков для матрицы выигрышей (13.6):

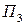
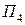
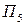
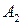
(13.7)

Матрица рисков проясняет некоторые нюансы рассматриваемой игры с природой. Так, если игрок А выбрал стратегию А₆ (см. матрицу выигрышей (13.6)), то при состояниях природы и 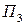он получает одинаковые выигрыши 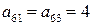. Однако эти выигрыши не являются равноценными в смысле рисков, поскольку удачность выбора стратегии А₆ по отношению к состояниям природы и 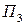разная. Благоприятность состояния природы для возможности увеличения выигрыша равна , а состояния 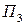- равна 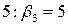(см. последнюю строку матрицу (13.6)). Поэтому риски игрока А при выборе стратегии А₆ и при состояниях природы и 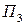соответственно равны и (см. матрицу рисков (13.7)). Другими словами, при состоянии природы игрок А мог выиграть по максимуму 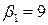единиц выигрыша, а выбрав стратегию А₆ , выиграл всего 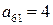единиц, потеряв возможных единиц. При состоянии природы 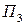игрок А мог выиграть максимум 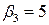единиц выигрыша, а выиграл, придерживаясь стратегии А₆ ,единицы, потеряв всего единицу. Таким образом, выбор стратегии А₆ по отношению к состоянию природы 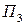более удачлив, чем по отношению к состоянию природы . Именно эту ситуацию и отражает матрица рисков (13.7).

Матрица выигрышей (13.6) однозначно определяет матрицу рисков (13.7). Обратное, однако, неверно.

В теории игр с природой в зависимости от имеющейся или добываемой информации различают две ситуации. Одна из них характеризуется тем, что либо известны вероятности, с которыми природа принимает каждое из своих возможных состояний, либо эти вероятности не известны, но имеются сведения об их относительных значениях, либо вероятности состояний природы устанавливаются в результате опроса экспертов и усреднения их показаний. В этой ситуации говорят о "принятии решения в условиях риска". В другой ситуации вероятности возможных состояний природы неизвестны и нет никакой возможности получить о них какую-либо информацию. В этом случае говорят о "принятии решения в условиях неопределенности".