Гидравлический удар. Переходные процессы.
Пусть имеется труба длины  и диаметром
и диаметром 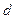 , заполненная некоторой жидкостью; на одном из концов трубы расположен затвор (задвижка). Будем считать, что первоначально жидкость движется по трубе в сторону затвора, а затвор полностью открыт. В случае если в какой-либо следующий момент времени затвор мгновенно закрыть (или открыть, если жидкость первоначально покоилась в трубе), то для расчета инерционного давления вблизи затвора необходимо принимать в расчет сжимаемость жидкости и упругость стенок трубы. Картина движения жидкости вблизи затвора будет следующая. При мгновенном закрытии слой жидкости, примыкающий к затвору, должен остановиться, а давление резко увеличиться, но если жидкость сжимаемая, мгновенной остановки не происходит, вдоль по жидкости начнут распространяться возмущения, обусловленные резким торможением. Импульсы возмущений будут распространяться со скоростью звука. Возмущения, проходя те участки, по которым прошли предыдущие импульсы и нагрели среду, приобретают большую скорость. Поэтому последующие возмущения догоняют предыдущие и приводят вблизи затвора к резкому повышению давления, которое называется гидравлическим ударом.
, заполненная некоторой жидкостью; на одном из концов трубы расположен затвор (задвижка). Будем считать, что первоначально жидкость движется по трубе в сторону затвора, а затвор полностью открыт. В случае если в какой-либо следующий момент времени затвор мгновенно закрыть (или открыть, если жидкость первоначально покоилась в трубе), то для расчета инерционного давления вблизи затвора необходимо принимать в расчет сжимаемость жидкости и упругость стенок трубы. Картина движения жидкости вблизи затвора будет следующая. При мгновенном закрытии слой жидкости, примыкающий к затвору, должен остановиться, а давление резко увеличиться, но если жидкость сжимаемая, мгновенной остановки не происходит, вдоль по жидкости начнут распространяться возмущения, обусловленные резким торможением. Импульсы возмущений будут распространяться со скоростью звука. Возмущения, проходя те участки, по которым прошли предыдущие импульсы и нагрели среду, приобретают большую скорость. Поэтому последующие возмущения догоняют предыдущие и приводят вблизи затвора к резкому повышению давления, которое называется гидравлическим ударом.
Получим формулу для расчета инерционного (ударного) повышения давления. При полном торможении столба жидкости в трубе освобождающаяся кинетическая энергия 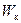 затрачивается на работу деформации (растяжения) стенок трубы
затрачивается на работу деформации (растяжения) стенок трубы 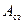 и работу деформации (сжатия) столба жидкости
и работу деформации (сжатия) столба жидкости 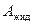 :
:
 (7.96)
(7.96)
Кинетическая энергия жидкости в трубе равна
 (7.97)
(7.97)
где 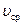 – средняя скорость потока до закрытия,
– средняя скорость потока до закрытия,  – плотность жидкости,
– плотность жидкости, 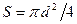 – площадь сечения столба жидкости длиной
– площадь сечения столба жидкости длиной  . Работа деформации равна потенциальной энергии деформированного тела и составляет половину произведения силы на удлинение. Работа сил деформации, приложенных к стенкам трубы при ударном повышении давления на величину
. Работа деформации равна потенциальной энергии деформированного тела и составляет половину произведения силы на удлинение. Работа сил деформации, приложенных к стенкам трубы при ударном повышении давления на величину 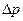 , может быть представлена как работа сил давления на толщине
, может быть представлена как работа сил давления на толщине 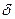 стенки трубы радиуса
стенки трубы радиуса  :
:
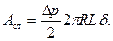 (7.98)
(7.98)
Согласно закону Гука, нормальное напряжение  материала стенки, характеризующегося модулем упругости
материала стенки, характеризующегося модулем упругости  , пропорционально относительному растяжению:
, пропорционально относительному растяжению:
 (7.99)
(7.99)
Связь напряжения в стенке и ударного повышения давления представим так:
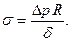
Из последних двух соотношений находим
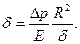 (7.100)
(7.100)
Подставляя (7.100) в (7.98), получим для работы деформации стенок трубы:
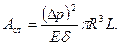 (7.101)
(7.101)
Работа сжатия жидкости объема 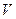 выражается как работа сил давления на пути
выражается как работа сил давления на пути 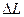 , по аналогии с (7.98):
, по аналогии с (7.98):
 (7.102)
(7.102)
Относительное изменение объема жидкости определяется через коэффициент сжимаемости

Подставляя в (7.102) изменение объема 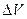 из последнего равенства и представляя объем столба жидкости как
из последнего равенства и представляя объем столба жидкости как 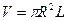 , получим следующее выражение для работы сжатия жидкости:
, получим следующее выражение для работы сжатия жидкости:
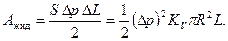 (7.103)
(7.103)
С учетом (7.97), (7.101) и (7.103) соотношение для энергии и работы, записанное в формуле (7.89), представляется так:
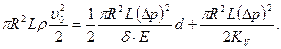
Отсюда после сокращения получаем формулу Н.Е. Жуковского для ударного давления при гидравлическом ударе:
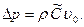 (7.104)
(7.104)
Здесь
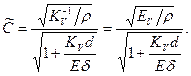 (7.105)
(7.105)
Величина 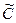 называется приведенной скоростью звука (скоростью ударной волны). Если стенки абсолютно жесткие, то
называется приведенной скоростью звука (скоростью ударной волны). Если стенки абсолютно жесткие, то 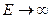 и скорость волны совпадает со скоростью звука в жидкости, равной
и скорость волны совпадает со скоростью звука в жидкости, равной 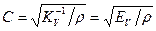 . С учетом этого формула для скорости ударной волны может быть преобразована в следующее выражение:
. С учетом этого формула для скорости ударной волны может быть преобразована в следующее выражение:
 (7.106)
(7.106)
Явление удара зависит от соотношения продолжительности (фазы) пробега волны к затвору и обратно  и быстроты закрытия затвора
и быстроты закрытия затвора  . Рассмотрим два характерных случая переходных процессов при гидравлическом ударе.
. Рассмотрим два характерных случая переходных процессов при гидравлическом ударе.
1. Предположим, что  . В этой ситуации гидравлический удар является прямым, закрытие происходит раньше, чем вода дойдет до затвора. Повышение давления следует рассчитывать по формуле Жуковского.
. В этой ситуации гидравлический удар является прямым, закрытие происходит раньше, чем вода дойдет до затвора. Повышение давления следует рассчитывать по формуле Жуковского.
2. Второй случай относится к непрямому удару, когда к неуспевшему закрыться крану подходит волна, уменьшающая рост давления. В этой ситуации время закрытия задвижки велико:  . Величина гидравлического непрямого удара определяется следующей формулой:
. Величина гидравлического непрямого удара определяется следующей формулой:
 (7.107)
(7.107)
При  формула (7.107) переходит в формулу Жуковского. В предельном случае бесконечно медленного закрытия задвижки,
формула (7.107) переходит в формулу Жуковского. В предельном случае бесконечно медленного закрытия задвижки,  , ударное повышение давления стремится к нулю:
, ударное повышение давления стремится к нулю: 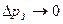 .
.
К числу широко распространенных средств борьбы с гидравлическим ударом относятся змеевики и гасители камерного типа. Фундаментальные работы в области применения методов нелинейной волновой механики к технологии стабилизаторов внезапного повышения давления выполнены академиком РАН Р.Ф. Ганиевым (род. 1937). Промышленные испытания показали, что стабилизаторы снижают давление гидроудара на  , а скорость нарастания давления при аварийных отключениях насосных агрегатов может быть понижена на порядок.
, а скорость нарастания давления при аварийных отключениях насосных агрегатов может быть понижена на порядок.