Алгоритм нейронного газа

Значительно лучшую самоорганизацию сети и ускорение сходимости алгоритма WTM можно получить применением метода, предложенного в [7] и названного авторами алгоритмом нейронного газа из-за подобия его динамики движению молекул газа.

В этом алгоритме на каждой итерации все нейроны сортируются в зависимости от их расстояния до вектора x. После сортировки нейроны размечаются в последовательности, соответствующей увеличению удаленности

, (5.20)

где обозначает удаленность i-го нейрона, занимающего в результате сортировки m-ю позицию в последовательности, возглавляемой нейроном-победителем, которому сопоставлена удаленность . Значение функции соседства для i-го нейрона определяется по формуле

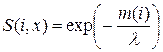, (5.21)

в которой обозначает очередность, полученную в результате сортировки (=0,1,2,…,K-1), а 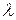– параметр, аналогичный уровню соседства в алгоритме Кохонена, уменьшающийся с течением времени. При 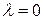адаптации подвергается только нейрон-победитель, и алгоритм превращается в обычный алгоритм WTA, но при уточнению подлежат веса многих нейронов, причем уровень уточнения зависит от величины . Алгоритм нейронного газа напоминает стратегию нечетких множеств, в соответствии с которой каждому нейрону приписывается значение функции принадлежности к окрестности, определенной отношением (5.19).

Для достижения хороших результатов самоорганизации процесс обучения должен начинаться с большого значения 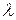, однако с течением времени его величина уменьшается до нуля. Изменение может быть линейным или показательным. Предложено изменять значение в соответствии с выражением

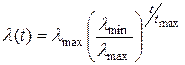, (5.22)

где обозначает значение 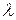на t-й итерации, а 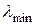и 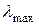– принятые минимальное и максимальное значения 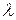соответственно. Коэффициент определяет максимальное заданное количество итераций.

Коэффициент обучения i-го нейрона тоже может изменяться как линейно, так и показательно, причем его степенная изменчивость определяется формулой

, (5.23)

в которой обозначает начальное значение коэффициента обучения, – априорно заданное минимальное значение, соответствующее . На практике наилучшие результаты самоорганизации достигаются при линейном изменении .

Для сокращения объема вычислений, необходимых для реализации алгоритма нейронного газа, можно применить определенное упрощение, состоящее в учете при сортировке только нейронов с наиболее значимой величиной функции . При этом используется зависимость (5.20), в соответствии с которой если , то значение .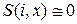

Алгоритм нейронного газа наряду с алгоритмом WTA, учитывающим активность нейронов, считается одним из наиболее эффективных средств самоорганизации нейронов в сети Кохонена. При соответствующем подборе параметров управления процессом можно добиться очень хорошей организации сети при скорости функционирования, превышающей скорость, достижимую в классическом алгоритме Кохонена.