Сигмоидальный нейрон

Нейрон сигмоидального типа имеет структуру, подобную модели МакКаллока–Питса, с той разницей, что функция активации является непрерывной и может быть выражена в виде сигмоидальной униполярной или биполярной функции [4]. Структура нейрона представлена на рис. 2.6.

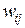Входные сигналы (j=1,2,…,N) суммируются с учетом соответствующих весов (сигнал поступает в направлении от узла j к узлу i) в сумматоре, после чего результат сравнивается с пороговым значением . Выходной сигнал нейрона y_i определяется при этом зависимостью

. (2.9)

Аргументом функции выступает суммарный сигнал . Функция f(u_i), называемая функцией активации, относится к классу непрерывных, монотонно возрастающих и дифференцируемых функций. Нейрон сигмоидального типа использует сигмоидальную униполярную (логистическую) или сигмоидальную биполярную (гиперболический тангенс) функцию активации.

Рис. 2.6 Модель сигмоидального нейрона

Униполярная функция, как правило, представляется формулой

, (2.10)

тогда как биполярная функция задается в виде (2.11) или (2.12):

. (2.11)

(2.12)

Графики сигмоидальных функций при k=1 представлены на рис. 2.7.

Отметим, что, как правило, современные компьютеры вычисляют функцию гиперболического тангенса быстрее, чем логистическую. Другое преимущество функции гиперболического тангенса состоит в том, что она изменяется в диапазоне от –1 до +1. Часто бывает необходимо нормировать обучающий набор данных таким образом, чтобы среднее значение было равно 0 при единичном стандартном отклонении.

Такая нормировка возможна только с функцией активации, которая способна принимать отрицательные значения. И наконец, нечетная функция, такая, как гиперболический тангенс, обеспечивает более быстрое обучение, чем несимметричная логистическая функция.

В этих формулах параметр k подбирается пользователем. Его значение влияет на форму функции активации. При малых значениях k график функции достаточно пологий, по мере роста значения k крутизна графика увеличивается.

 

Рис. 2.7 Графики сигмоидальных функций:
а – логистическая; б – гиперболический тангенс

При k → ∞ сигмоидальная функция превращается в пороговую функцию, идентичную функции активации персептрона. На практике чаще всего для упрощения используется значение k =1.

Важным свойством сигмоидальной функции является ее дифференцируемость. Для униполярной функции имеем

, (2.13)

тогда как для биполярной функции

. (2.14)

И в первом, и во втором случае график изменения производной относительно переменной x имеет колоколообразную форму, а его максимум соответствует значению x=0.

Сигмоидальный нейрон, как правило, обучается с учителем.

При обучении с учителем предполагается, что помимо входных сигналов, составляющих вектор x, известны также и ожидаемые выходные сигналы нейрона , составляющие вектор d. В подобной ситуации подбор весовых коэффициентов должен быть организован так, чтобы фактические выходные сигналы нейрона принимали бы значения, как можно более близкие к ожидаемым значениям . Ключевым элементом процесса обучения с учителем является знание ожидаемых значений выходного сигнала нейрона.

При обучении с учителем производится минимизация целевой функции, которая для единичного обучающего кортежа <x, d>i-го нейрона определяется в виде

(2.15)

где

. (2.16)

Применение непрерывной функции активации позволяет использовать при обучении градиентные алгоритмы. Проще всего реализовать метод наискорейшего спуска, в соответствии с которым уточнение вектора весов проводится в направлении отрицательного градиента целевой функции, при этом i-я составляющая градиента имеет вид:

(2.17)

(2.18)

Если ввести обозначение , то значения весовых коэффициентов могут быть уточнены дискретным способом в соответствии с формулой 2.19.

(2.19)

В данной формуле коэффициент – это коэффициент обучения, значение которого либо выбирают эмпирически из интервала (0,1), либо при помощи решения разностного уравнения, представленного формулой 2.20.

(2.20)

В данной формуле коэффициент 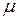выступает в роли аналогичной значению .

Формулы 2.19 и 2.20 определяют алгоритм обучения.

На эффективность обучения оказывает сильное влияние подбор коэффициентов обучения. В существующих алгоритмах обучения его величина может быть задана константой или переменной, значение которой в процессе обучения изменяется адаптивным способом либо подбирается на каждом шаге по принципу направленной минимизации целевой функции от одной переменной в направлении наискорейшего уменьшения значений этой целевой функции.

Необходимо подчеркнуть, что применение градиентного метода обучения гарантирует достижение только локального минимума. В случае полимодальной целевой функции, найденный локальный минимум может быть достаточно далек от глобального минимума. Для таких случаев может оказаться результативным обучение с моментом или разбросом. В этом методе процесс уточнения весов определяется не только информацией о градиенте функции, но также и фактическим трендом изменений весов. Приращение весов можно задать следующим математическим выражением:

, (2.21),

в котором первый член соответствует обычному методу наискорейшего спуска, а второй член (момент), отражает последнее изменение весов и не зависит от фактического значения градиента. Значение коэффициента момента ά, как правило, выбирается из интервала (0,1). С ростом значения ά увеличивается влияние момента на подбор весов.