Осевые (пропеллерные) насосы. 2 страница
| 1-корпус; 2-рабочее колесо; 3-направляющий аппарат; 4и 5-всасывающий и нагнетательный патрубки Рисунок 4.36 - Турбогазодувка |
В многоступенчатых турбогазодувках на валу устанавливают несколько колес с лопатками (обычно 3-4), причем газ между ступенями не охлаждается. Диаметры колес в многоступенчатой турбогазодувке постоянны, но ширина их снижается в направлении от первого колеса к последнему. Этим достигается возможность сжатия в каждой последующей ступени без изменения числа оборотов вала и формы лопаток рабочих колес. Степень сжатия в турбогазодувках не превышает 3-3,5.
Турбокомпрессорыпо устройству аналогичны турбогазодувкам, но создают более высокие степени сжатия. В них устанавливают большее число колес, чем в турбогазодувках, причем колеса имеют разный диаметр (диаметр и ширина колеса уменьшаются от первого колеса к последнему). Часто рабочие колеса турбокомпрессоров секционируют и располагают их в двух или трех корпусах. В пре-. делах каждого корпуса колеса имеют одинаковый диаметр, но разную ширину. При этом обычно газ между корпусами охлаждают в промежуточных холодильниках. Давление нагнетания в центробежных турбокомпрессорах достигает 2,5-3,0 МПа.
Осевые компрессоры. Корпус осевого вентилятора изготовляют в виде короткого цилиндрического патрубка 1(рисунок 4.37), в котором вращается рабочее колесо 2(в виде пропеллера с лопатками). Воздух движется прямотоком вдоль оси вала, вследствие чего к.п.д. осевых вентиляторов существенно выше, чем центробежных (снижается гидравлическое сопротивление самого вентилятора). Однако напор, развиваемый осевыми вентиляторами, значительно ниже, чем развиваемый центробежными (в 3-4 раза).

| 1-корпус; 2-рабочее колесо Рисунок 4.37 - Осевой (пропеллерный) вентилятор |
4.8 Гидромеханические процессы
Гидромеханическими называются процессы, предназначены для разделения неоднородных систем.
4.8.1 Понятие неоднородной системы; способы разделения
Неоднородной считается система, состоящая из двух или более фаз. Любую неоднородную систему можно представить состоящей из дисперсионной (сплошной или основной) фазы и дисперсной (прерывистой) фазы.
Основной объем неоднородной системы занимает дисперсионная фаза.
В зависимости от физического состояния фаз различают неоднородные системы, представленные в таблице 4.3.
Таблица 4.3 – Виды неоднородных систем
| Вид неоднородной системы | Дисперсионная фаза | Дисперсная фаза |
| Суспензия | жидкость | твердые частицы |
| Эмульсия | жидкость | жидкость |
| Пыль | газ | твердые частицы |
| Туман | газ | жидкость |
| Пена | жидкость | газ |
Неоднородная система, в которой дисперсионная фаза является газом, называют газовыми суспензии, или аэродисперсными системами, а если газ-воздух, то аэрозолями.
В зависимости от размеров частиц суспензии условно подразделяют на
- грубые (с частицами размером более 100 мкм);
- тонкие (содержат частицы размером 0,1…100 мкм);
- коллоидные растворы (с частицами менее 0,1 мкм).
Аэродисперсные системы по размеру частиц условно подразделяют на
- пыль (с частицами размером 5…50 мкм);
- дым (с частицами размером менее 5 мкм).
Для разделения неоднородных систем применяют следующие основные методы
- осаждение под действием
-- силы тяжести (отстаивание);
-- центробежной силы (циклонный процесс или центрифугирование);
-- электростатических сил (электроосаждение);
- фильтрование под действием разности давлений, создаваемой
-- нагнетательными машинами (насосы, компрессоры);
-- центробежными силами (центробежное фильтрование);
- мокрая очистка газов – орошение жидкостью для осаждения и коагуляции (слипания) частиц.
Выбор метода разделения зависит от концентрации дисперсных частиц, их размера, требований к качеству разделения, а также от разницы плотностей дисперсной и сплошной фаз и вязкости последней.
4.8.2 Материальный баланс процессов разделения
Материальный баланс процессов разделения рассмотрим на примере разделения суспензии. Продуктами разделения являются осветленная жидкость (очищенная сплошная фаза) и осадок (сгущенная дисперсная фаза).
Обозначим
 ,
, ,
, - массовый расход соответственно исходной (начальной) суспензии, осветленной жидкости и осадка, кг/с;
- массовый расход соответственно исходной (начальной) суспензии, осветленной жидкости и осадка, кг/с;
 ,
, ,
, - концентрация дисперсной фазы соответственно в исходной суспензии, осветленной жидкости и осадке, массовые доли.
- концентрация дисперсной фазы соответственно в исходной суспензии, осветленной жидкости и осадке, массовые доли.
При отсутствии потерь вещества в процессе разделения можно записать следующие уравнения материального баланса
- по внешним потокам:
 ; (4.115)
; (4.115)
- по дисперсной фазе:
 . (4.116)
. (4.116)
Система уравнений (4.115) и (4.116) позволяет выполнить материальный расчет, т.е. по известным значениям расхода исходной суспензии и концентраций определить  и
и 
 ;
;  . (4.117)
. (4.117)
Более простыми будут выражения (4.116) и (4.117) в случае отсутствия дисперсных частиц в очищенной жидкости ( =0), что возможно при эффективности разделения, равной 100%. В этом случае уравнение материального баланса по внешним потокам записывается в виде выражения (4.115), а по дисперсной фазе – в виде уравнения
=0), что возможно при эффективности разделения, равной 100%. В этом случае уравнение материального баланса по внешним потокам записывается в виде выражения (4.115), а по дисперсной фазе – в виде уравнения
 . (4.118)
. (4.118)
Тогда
 ;
;  . (4.119)
. (4.119)
Иногда в процессе расчета аппаратов для разделения неоднородных систем необходимо определить объемный расход (V) продуктов разделения, который связан с массовым расходом выражением
 , м
, м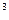 /с, (4.120)
/с, (4.120)
где  - плотность кг/ м
- плотность кг/ м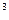 .
.
Плотность неоднородной системы  при ее составе, выраженном в массовых долях, можно рассчитать по выражению
при ее составе, выраженном в массовых долях, можно рассчитать по выражению
 , (4.121)
, (4.121)
где X – концентрация дисперсной фазы в системе;
 и
и  - плотность соответственно частиц и жидкости.
- плотность соответственно частиц и жидкости.
С учетом уравнений (4.120) и (4.121) объемный расход осадка (м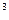 /с)
/с)
 ; (4.122)
; (4.122)
 . (4.123)
. (4.123)
4.8.3 Отстаивание. Теоретические основы процесса
Отстаивание применяют в промышленности для сгущения суспензий или классификации суспензий по фракциям частиц твердой фазы, для грубой очистки газов от пылей и для разделения эмульсий.
Важным показателем процесса отстаивания является скорость осаждения частиц под действием силы тяжести. Для этого рассмотрим поведение твердой частицы в жидкой среде.  и
и  соответственно плотность частиц и среды.
соответственно плотность частиц и среды.
Если  и
и  - плотность соответственно дисперсных частиц и среды, то в зависимости от соотношения этих величин поведение частиц будет различным. Если
- плотность соответственно дисперсных частиц и среды, то в зависимости от соотношения этих величин поведение частиц будет различным. Если  , то частица двигается вниз (осаждение); при
, то частица двигается вниз (осаждение); при  частица перемещается вверх (всплывает); при
частица перемещается вверх (всплывает); при  частица находится в относительном покое и разделить методом отстаивания такую систему не удается.
частица находится в относительном покое и разделить методом отстаивания такую систему не удается.
Рассмотри процесс осаждения сферической частицы диаметром d. На эту частицу, находящуюся в жидкости (рисунок 4.38), действует сила тяжести, равная весу частицы

 (4.124)
(4.124)
и подъемная сила, которая в соответствии с законом Архимеда равна весу жидкости, вытесненной частицей
 . (4.125)
. (4.125)
| Рисунок 4.38 – Схема сил, действующих на движущуюся в неподвижной среде частицу |
При осаждении частицы ( ) среда оказывает сопротивление движению, определяемое в общем случае законом Ньютона
) среда оказывает сопротивление движению, определяемое в общем случае законом Ньютона
 , (4.126),
, (4.126),
где  - безразмерный коэффициент сопротивления среды;
- безразмерный коэффициент сопротивления среды;
S – проекция частицы на плоскость, нормальную направлению движения, м . Для шарообразной частицы
. Для шарообразной частицы  ;
;
 - скорость движения частицы, м/с.
- скорость движения частицы, м/с.
Скорость движения частицы, соответствующая равновесию сил, называется скоростью свободного осаждения ( ).
).
Уравнение равновесия сил имеет вид
 . (4.127)
. (4.127)
Подставляя развернутые значения, получим
 , (4.128)
, (4.128)
откуда определяется скорость осаждения
 . (4.129)
. (4.129)
Однако, применение уравнения (4.129) в расчетной практике затруднительно, так как значение коэффициента сопротивления среды зависит от гидродинамического режима осаждения, который характеризуется критерием Рейнольдса ( ).
).
Для мелких частиц или при большой вязкости среды скорость осаждения мала и сопротивление среды проявляется в виде трения; такое безвихревое осаждение происходит при ламинарном режиме (рисунок 4.39,а). Предельные значения критерия  , соответствующие ламинарному движению, принимаются различными авторами от 0,2 до 2.
, соответствующие ламинарному движению, принимаются различными авторами от 0,2 до 2.

| а-при ламинарном режиме; б-при турбулентном режиме Рисунок 4.39 – Схема движения твердого тела в среде |
При осаждении в маловязкой среде сравнительно крупных частиц, приобретающих относительно большую скорость, сопротивление среды проявляется в основном в образовании турбулентных вихрей (рисунок 4.39,б). Такое осаждение происходит при турбулентном режиме. При этом  >500.
>500.
Возможен переходный режим осаждения, при котором величины сопротивления от трения и вихреобразования сопоставимы. При этом 2< <500.
<500.
Обработка методами теории подобия экспериментальных данных по исследованию обтекания сферических тел позволила получить следующие соотношения
- для ламинарного режима осаждения ( <2)
<2)
 ; (4.130)
; (4.130)
- для переходного режима осаждения (2< <500)
<500)
 ; (4.131)
; (4.131)
- для турбулентного режима осаждения ( >500)
>500)
 0,39…0,5. (4.132)
0,39…0,5. (4.132)
Подставляя в уравнение (4.129) значение  из выражения (4.130), для ламинарного режима получим закон осаждения Стокса
из выражения (4.130), для ламинарного режима получим закон осаждения Стокса
 , (4.133)
, (4.133)
где  - вязкость жидкости, Па*с.
- вязкость жидкости, Па*с.
Уравнение (4.133) можно использовать в расчетной практике с последующим уточнением гидродинамического режима осаждения.
Для получения обобщенного уравнения для определения скорости осаждения  из критерия
из критерия 
 (4.134)
(4.134)
и сравним с выражением (4.129). Равенство величин левой части уравнений предполагает равенство величин, стоящих в правой части. После вохведения в квадрат величин правой части уравнений (4.129) и (4.130) получим выражение
 ,
,
которое можно записать в виде
 ; (4.135)
; (4.135)
Безразмерный комплекс  является модификацией критерия Архимеда. Тогда уравнение (4.135) можно записать в виде
является модификацией критерия Архимеда. Тогда уравнение (4.135) можно записать в виде
 . (4.136)
. (4.136)
В состав определяющего критерия
 (4.137)
(4.137)
входят только величины, характеризующие суспензию, и легко определяемые по справочной литературе (плотность, вязкость).
Подставляя в уравнение (4.137) значения  из уравнений (4.130)-(4.132), можно определить режим и скорость осаждения.
из уравнений (4.130)-(4.132), можно определить режим и скорость осаждения.
При ламинарном режиме осаждения
 или
или  . (4.138)
. (4.138)
Область применения уравнения (4.138) легко определить, так как для границы ламинарного режима  <2, и в этом случае
<2, и в этом случае  36.
36.
Сделав аналогичные вычисления, получим
для переходного режима осаждения
 ;
;  ; (4.139)
; (4.139)
для турбулентного режима
 ;
;  . (4.140)
. (4.140)
Приближенное значение  (также для всех режимов движения частицы) можно найти по уравнению Тодеса
(также для всех режимов движения частицы) можно найти по уравнению Тодеса
 . (4.141)
. (4.141)
Графически определив критерий Лященко ( ) в зависимости от критерия Архимеда, можно также определить скорость осаждения частиц
) в зависимости от критерия Архимеда, можно также определить скорость осаждения частиц
 . (4.142)
. (4.142)
Графическая зависимость  для частиц различной формы (сферических, округлых и других) приведена в технической литературе.
для частиц различной формы (сферических, округлых и других) приведена в технической литературе.
Скорость свободного осаждения мелких капель можно определить по уравнению Адамара
 , (4.143)
, (4.143)
где  - плотность жидкостей, образующих соответственно дисперсную и сплошную фазу;
- плотность жидкостей, образующих соответственно дисперсную и сплошную фазу;
 - вязкость соответствующих жидкостей.
- вязкость соответствующих жидкостей.
Уравнение Адамара применимо, когда критерий Рейнольдса для капли  <1 (
<1 ( ).
).
Если  , уравнение (4.142) вырождается в уравнение Стокса (4.133).
, уравнение (4.142) вырождается в уравнение Стокса (4.133).
Приведенные расчетные выражения (уравнения (4.133), (4.138)-(4.143)) позволяют определить скорость свободного осаждения ( ), когда концентрация дисперсной фазы очень мала и ее частицы при движении не соприкасаются друг с другом.
), когда концентрация дисперсной фазы очень мала и ее частицы при движении не соприкасаются друг с другом.
В промышленности отстаивание применяют чаще всего в условиях высокой концентрации дисперсной фазы, когда происходит стесненное осаждение, скорость которого может быть значительно меньше скорости свободного осаждения. При этом вследствие трения между частицами и их взаимных столкновений наблюдается тенденция к сближению скоростей осаждения частиц различных размеров, возникает коллективное (стесненное) осаждение частиц со скоростями, близкими в каждом сечении аппарата, но различными по его высоте: с приближением к днищу аппарата скорость осаждения все более замедляется. Это связано с возникновением восходящих потоков жидкости из-за вытеснения ее осаждающимися на дно частицами. При этом процесс осложняется тем, что крупные частицы обгоняют мелкие. В условиях стесненного осаждения концентрация диспергированных частиц сильно изменяется по высоте отстойника: в верхней части располагается слой осветленной жидкости, ниже его – зона практически свободного осаждения, затем зона стесненного осаждения и, наконец, на дне находится слой осадка.
Скорость стесненного осаждения  является функцией скорости свободного осаждения и концентрации суспензии, которая в расчетных формулах выражается через объемную долю жидкости в суспензии
является функцией скорости свободного осаждения и концентрации суспензии, которая в расчетных формулах выражается через объемную долю жидкости в суспензии  :
:
 , (4.144)
, (4.144)
где  - объем соответственно сплошной и дисперсной фазы.
- объем соответственно сплошной и дисперсной фазы.
Для расчетов могут быть использованы следующие уравнения:
при 
 ; (4.145)
; (4.145)
при 
 . (4.146)
. (4.146)
На основе уравнений (4.145) и (4.146) можно рассчитать скорость стесненного осаждения одинаковых по размеру шарообразных частиц. При осаждении частиц иной формы полученное значение  следует умножить на поправочный коэффициент формы
следует умножить на поправочный коэффициент формы  , значения которого определяют опытным путем и для некоторых частиц приведены в таблице 4.4. Кроме того, при расчетах скоростей осаждения нешарообразных частиц в качестве их диаметра следует использовать диаметр эквивалентного шара.
, значения которого определяют опытным путем и для некоторых частиц приведены в таблице 4.4. Кроме того, при расчетах скоростей осаждения нешарообразных частиц в качестве их диаметра следует использовать диаметр эквивалентного шара.
Расчет скоростей осаждения для суспензий, содержащих частицы различного диаметра, не может быть выполнен с достаточной точностью. В этих случаях необходима постановка экспериментов.
Таблица 4.4 – Значения коэффициента формы частиц 
| Форма частицы | Значение коэффициента 
|
| Сферическая | |
| Округлая | 0,77 |
| Пластинчатая | 0,73 |
| Угловатая | 0,66 |
| Продолговатая | 0,58 |
Схема расчета скорости стесненного осаждения
1 Определяется критерий Архимеда (уравнение (4.137));
2 По значению  определяется гидродинамический режим осаждения и выбирается расчетная формула для числа Рейнольдса (уравнения (4.138)-(4.140));
определяется гидродинамический режим осаждения и выбирается расчетная формула для числа Рейнольдса (уравнения (4.138)-(4.140));
3 По уравнению (4.134) определяется скорость свободного осаждения частицы ( );
);
4 По уравнениям (4.145) либо (4.146) с учетом коэффициента формы частицы рассчитывается скорость стесненного осаждения.
4.8.4 Классификация аппаратов для отстаивания. Конструкции
Аппараты для осаждения под действием силы тяжести называются отстойниками.
По принципу действия отстойники можно разделить на три типа
- аппараты непрерывного действия, в которые постоянно подается неоднородная система и постоянно выводятся продукты разделения;
- аппараты периодического действия, в которые подается неоднородная система и находится в аппарате в течение времени, достаточном для осаждения частиц, затем продукты разделения выводится;
- аппараты смешанного действия, в которые неоднородная система подается постоянно, постоянно выводится очищенная сплошная фаза, а осадок удаляется периодически по мере накопления.
По конструкции все отстойники можно разделить на
- горизонтальные;
- вертикальные;
- с гребковой мешалкой;
- с коническими полками и другие.
По виду неоднородной системы различают отстойники
- для разделения эмульсий;
- для разделения газовых суспензий (пылеосадительная камера);
- для разделения жидких суспензий.
Рассмотрим наиболее применяемые в химической технологии конструкции отстойников.
| 1-корпус; 2-днище; 3-гребковая мешалка; 4-кольцевой желоб Рисунок 4.40 - Отстойник непрерывного действия с гребковой мешалкой |
 Широко распространены отстойники непрерывного действия с гребковой мешалкой (рисунок 4.40). Они представляют собой цилиндрический резервуар 1с коническим днищем 2. В резервуаре установлена мешалка 3,снабженная гребками, которые непрерывно перемещают осадок к центральному разгрузочному отверстию и одновременно слегка взбалтывают осадок, способствуя его обезвоживанию. Частота вращения мешалки незначительна (0,02-0,5 об/мин), поэтому процесс осаждения не нарушается. Суспензия непрерывно поступает по трубе в середине резервуара. Осветленная жидкость переливается в кольцевой желоб 4и удаляется через штуцер. Осадок (шлам), представляющий собой сгущенную суспензию, удаляется через штуцер в коническом днище с помощью диафрагмового насоса. Вал мешалки приводится во вращение от электродвигателя через редуктор.
Широко распространены отстойники непрерывного действия с гребковой мешалкой (рисунок 4.40). Они представляют собой цилиндрический резервуар 1с коническим днищем 2. В резервуаре установлена мешалка 3,снабженная гребками, которые непрерывно перемещают осадок к центральному разгрузочному отверстию и одновременно слегка взбалтывают осадок, способствуя его обезвоживанию. Частота вращения мешалки незначительна (0,02-0,5 об/мин), поэтому процесс осаждения не нарушается. Суспензия непрерывно поступает по трубе в середине резервуара. Осветленная жидкость переливается в кольцевой желоб 4и удаляется через штуцер. Осадок (шлам), представляющий собой сгущенную суспензию, удаляется через штуцер в коническом днище с помощью диафрагмового насоса. Вал мешалки приводится во вращение от электродвигателя через редуктор.
 Отстойники с гребковой мешалкой обеспечивают однородность осадка, позволяют обезводить его до концентрации твердой фазы 35-55%; работа таких отстойников полностью автоматизирована. К недостаткам этих аппаратов следует отнести их громоздкость.
Отстойники с гребковой мешалкой обеспечивают однородность осадка, позволяют обезводить его до концентрации твердой фазы 35-55%; работа таких отстойников полностью автоматизирована. К недостаткам этих аппаратов следует отнести их громоздкость.
Диаметр нормализованных аппаратов от 1,8 до 30 м; в отдельных случаях применяют отстойники диаметром до 100 м. Для уменьшения площади, занимаемой отстойниками, применяют многоярусные аппараты, представляющие собой несколько отстойников, поставленных друг на друга и имеющих общий вал для гребковых мешалок. Многоярусность существенно усложняет конструкцию аппарата.
| Рисунок 4.41 - Отстойник непрерывного действия с коническими полками |
Несложны по конструкции и обладают большой поверхностью отстойники непрерывного действия с коническими полками (рисунок 4.41). Поступающая в аппарат суспензия распределяется по каналам между коническими полками, на поверхности которых осаждаются твердые частицы. Осадок сползает по наклонным полкам к стенкам корпуса и затем перемещается в нижнюю часть аппарата, откуда удаляется. Осветленная жидкость поступает в центральную трубу и выводится из верхней части аппарата.
Помимо большой поверхности осаждения к достоинствам отстойников этого типа относятся отсутствие движущихся частей и простота обслуживания. Однако влажность шлама в них больше, чем в отстойниках с гребковой мешалкой.
| 1 - корпус; 2-перфорированная перегородка Рисунок 4.42 - Отстойник непрерывного действия для разделения эмульсий |
 На рисунке 4.42 показан отстойник непрерывного действия для разделения эмульсий. Он представляет собой горизонтальный резервуар с перфорированной перегородкой 2,которая предотвращает возмущение жидкости в отстойнике струей эмульсии, поступающей в аппарат. Поперечное сечение отстойника выбирают таким, чтобы скорость течения жидкости в корпусе 1аппарата не превышала нескольких миллиметров в секунду, и режим течения был ламинарным, что предупреждает смешение фаз и улучшает процесс отстаивания. Расслоившиеся легкая и тяжелая фазы выводятся с противоположной стороны отстойника. Трубопровод для вывода тяжелой фазы соединен с атмосферой для предотвращения засифонивания.
На рисунке 4.42 показан отстойник непрерывного действия для разделения эмульсий. Он представляет собой горизонтальный резервуар с перфорированной перегородкой 2,которая предотвращает возмущение жидкости в отстойнике струей эмульсии, поступающей в аппарат. Поперечное сечение отстойника выбирают таким, чтобы скорость течения жидкости в корпусе 1аппарата не превышала нескольких миллиметров в секунду, и режим течения был ламинарным, что предупреждает смешение фаз и улучшает процесс отстаивания. Расслоившиеся легкая и тяжелая фазы выводятся с противоположной стороны отстойника. Трубопровод для вывода тяжелой фазы соединен с атмосферой для предотвращения засифонивания.
| 1-корпус; 2-полки; 3-отражательная перегородка; 4-люки для удаления пыли Рисунок 4.43 - Пылеосадительная камера |
 Очистку газов от пыли под действием сил тяжести проводят в пылеосадителъных камерах (рисунок 4.43). Запыленный газ поступает в корпус камеры 7, в котором установлены горизонтальные полки 2. Расстояние между полками составляет 100-300 мм. Газ проходит в каналах между полками, при этом на поверхности последних осаждается пыль. Пройдя полки, газ огибает вертикальную отражательную перегородку 3и удаляется из камеры. Основное назначение перегородки 3 -обеспечить равномерное распределение газа между полками; кроме того, при огибании газом перегородки из него под действием сил инерции удаляется часть пыли. Осевшая на полках пыль периодически удаляется с помощью скребков через люки 4или же смывается водой.
Очистку газов от пыли под действием сил тяжести проводят в пылеосадителъных камерах (рисунок 4.43). Запыленный газ поступает в корпус камеры 7, в котором установлены горизонтальные полки 2. Расстояние между полками составляет 100-300 мм. Газ проходит в каналах между полками, при этом на поверхности последних осаждается пыль. Пройдя полки, газ огибает вертикальную отражательную перегородку 3и удаляется из камеры. Основное назначение перегородки 3 -обеспечить равномерное распределение газа между полками; кроме того, при огибании газом перегородки из него под действием сил инерции удаляется часть пыли. Осевшая на полках пыль периодически удаляется с помощью скребков через люки 4или же смывается водой.
Хотя поверхность осаждения при большом числе полок может быть достаточно велика, степень очистки газа от пыли в этих аппаратах обычно не превышает 30-40%, причем частицы размером 5 мкм и меньше вообще не отделяются от газа. Поэтому пылеосадительные камеры используют для предварительной грубой очистки сильно запыленных газов, содержащих частицы размером не менее нескольких десятков микрометров.