Наибольшее и наименьшее значения функции в замкнутой области

Пусть функция определена и непрерывна в ограниченной замкнутой области . Тогда она достигает в некоторых точках своего наибольшего М и наименьшего m значений (т. н. глобальный экстремум). Эти значения достигаются функцией в точках, расположенных внутри области , или в точках, лежащих на границе области.

Правило нахождения наибольшего и наименьшего значений дифференцируемой в области функции состоит в следующем:

1. Найти все критические точки функции, принадлежащие , и вычислить значения функции в них;

2. Найти наибольшее и наименьшее значения функции на границах области;

3. Сравнить все найденные значения функции и выбрать из них наибольшее М и наименьшее m.

Пример 2. Найти наибольшее и наименьшее значения функции в замкнутой области, ограниченной линиями: (рис.2).

 

Рис. 2

 

Решение: Здесь , .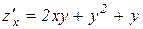

1. Находим все критические точки:

Решением системы являются точки (0,0), (-1,0), (0,-1), .

Ни одна из найденных точек не принадлежит области .

 

2. Исследуем функцию z на границе области, состоящей из участков АВ, ВС, СЕ и ЕА (рис. 2).

На участке АВ: где , , 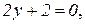у= –1.

Значения функции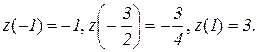

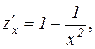
На участке ВC: где , Значения функции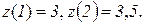

На участке CE: где , , Значения функции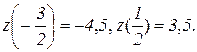

На участке АE: 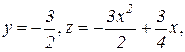где ,

Значения функции

 

3. Сравнивая полученные результаты, имеем: а

 

 

В некоторых вопросах математики и её приложений часто приходится решать задачи на отыскание локальных экстремумов функции не на всем множестве её задания, а только на некотором его подмножестве, в частности, на некоторой линии L, целиком принадлежащей данному множеству. Такие экстремумы называются условными (в отличие от ранее рассмотренных, называемых безусловными), так как в таких случаях налагаются дополнительные условия на характер изменения переменных.