Вольт-фарадная характеристика p-n перехода

ВАХ описывает связь между I и U на p-n переходе в статическом режиме. Эти уравнения могут быть использованы для определения I перехода и при воздействии переменного U , изменяющегося с небольшой скоростью. Но они теряют силу при быстром изменении напряжения, соизмеримом по длительности цикла с временем накопления и рассасывания неравновесного носителя заряда в базе. Такой режим называют динамическим.

В динамическом режиме p-n переход является инерционным элементом по отношению к быстрым изменениям тока или напряжения, поскольку новое распределение носителей устанавливается не сразу. Во-первых, внешнее напряжение меняет ширину перехода, а значит, и величину пространственных зарядов в переходе, во-вторых, при инжекции и экстракции меняются заряды в квазинейтральной области базы. Следовательно, наряду с проводимость, которая в первом приближении характеризуется выражением , p-n переход обладает емкостью, которую можно считать подключенной параллельно переходу. Эту емкость принято разделять на две составляющие: барьерную емкость Сбар, отражающую перераспределение зарядов в переходе, и диффузионную емкость Сдиф, отражающую перераспределение носителей зарядов в базе.

Изменение внешнего напряжения dU на p-n переходе приводит к изменению накопленного в нем заряда dQ. Поэтому р-n переход ведет себя подобно конденсатору, емкость которого C=dQ/dU.

В зависимости от физической природы изменяющегося заряда различают емкости зарядную (барьерную) и диффузионную.

Барьерная емкость определяется изменением нескомпенсированного заряда ионов при изменении ширины запирающего слоя под воздействием внешнего обратного напряжения. Поэтому идеальный электронно-дырочный переход можно рассматривать как плоский конденсатор, емкость которого определяется соотношением

С_бар = εП/δ,

где П, δ – соответственно площадь и толщина р-n-перехода.

Кроме того,

В общем случае зависимость зарядной емкости от приложенного к р-n-переходу обратного напряжения выражается формулой

где С₀ – емкость р-n-перехода при U_обр= 0; γ – коэффициент, зависящий от типа р-n-перехода (для резких р-n-переходов γ = 1/2, а для плавных γ = 1/3).

Барьерная емкость увеличивается с ростом N_а и N_д, а также с уменьшением обратного напряжения. Характер зависимости С=f(U_обр) показан на рис. 6.

Рис. 6. Зависимость барьерной емкости от внешнего напряжения

 

Одна из принципиальных особенностей, отличающих емкость Сбар от емкости плоского конденсатора, состоит в том, что в переходе направление вектора напряженности электрического поля не зависит от полярности приложенного напряжения.

Оценим значение Сбар для кремниевого p-n перехода, полагая l₀ = 0,5 мкм; φ_К = 0,75 В; S = 1 мм² и U_обр = 10 В; тогда Сбар ≈ 10 пФ.

Рассмотрим диффузионную емкость. При увеличении внешнего напряжения, приложенного к р-n-переходу в прямом направлении, растет концентрация инжектированных носителей вблизи границ перехода, что приводит к изменению количества заряда, обусловленного неосновными носителями в р- и n-областях. Это можно рассматривать как проявление некоторой емкости. Поскольку она зависит от изменения диффузионной составляющей тока, то её называют диффузионной. Диффузионная емкость представляет собой отношение приращения инжекционного заряда dQ_инж к вызвавшему его изменению напряжения dU_пр, т.е.

С_диф = dQ_инж / dU_пр.

Можно определить заряд инжектированных носителей, например дырок в n-области:

Тогда диффузионная емкость, обусловленная изменением общего заряда неравновесных дырок в n-области, определится по формуле

Аналогично для диффузионной емкости, обусловленной инжекцией электронов в p-область,

Общая диффузионная емкость

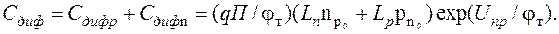
Оценим значение Сдиф при Iпр = 10 мА и τ = 10^-5 с, тогда Сдиф = 4 мкФ.

Полная емкость р-n-перехода определяется суммой барьерной и диффузионной емкостей: С_пер = С_бар + С_диф.

При включении р-n-перехода в прямом направлении преобладает диффузионная емкость, а при включении в обратном направлении – барьерная.

Вольт-фарадная характеристика – это зависимость емкости p-n перехода от напряжения, приложенного к нему. Эта характеристика представлена на рис. 7.

Рис. 7. Вольт-фарадная характеристика