Сущность регрессионного анализа. Уравнение регрессии. Метод наименьших квадратов

Регрессионный анализ заключается в определении аналитической формы связи, в которой изменение результативного признака обусловлено влиянием одного или нескольких факторных признаков, а множество всех прочих факторов, также оказывающих влияние на результативный признак, принимается за постоянные и средние значения. До регрессионного анализа следует проводить корреляционный анализ, в процессе которого оценивается степень тесноты статистической связи между исследуемыми переменными. От степени тесноты связи зависит прогностическая сила регрессионной модели.

Целью регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака от факторных признаков.

Уравнение регрессии или модель связи социально-экономических явлений выражается функцией. Различают парную () и множественную () регрессии.

Парная регрессий описывает связь между двумя признаками (результативным и факторным). Множественная регрессия описывает связь между результативным признаком и двумя и более факторными признаками.

Изучение модели парной регрессии является базовым во всем курсе эконометрики. Обычно она применяется в том случае, когда из всего круга факторов, влияющих на результат, можно выделить один, оказывающий наиболее сильное воздействие. Он и берется в качестве объясняющей переменной х.

Представим, что есть два ряда данных:

x₁	x₂	x₃	…	х_n
y₁	y₂	y₃	…	y_n

где n – число наблюдений.

Каждое из наблюдений характеризуется двумя переменными x_i, y_i. Число наблюдений n должно в шесть-семь раз превышать число параметров при переменной х в уравнении регрессии. Таким образом, для изучения линейной регрессии число наблюдений должно быть не менее семи.

В парной линейной регрессии связь между переменными определяется следующим образом:

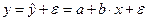где у – зависимая (объясняемая) переменная, реальная, фактическая, эмпирическая;

х – независимая (объясняющая) переменная;

– зависимая переменная, рассчитанная по уравнению регрессии, теоретическая;

а, b – константы, параметры уравнения линейной регрессии;

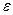– случайная компонента, возмущение.

Каждую пару наблюдений (х_i;y_i) можно представить в виде точки на плоскости. Такое графическое изображение наблюдений называется полем корреляции или диаграммой рассеяния. Выбранный тип функции (прямая, парабола, гипербола и т.д.) должен проходить через большее количество точек или как можно ближе к ним.

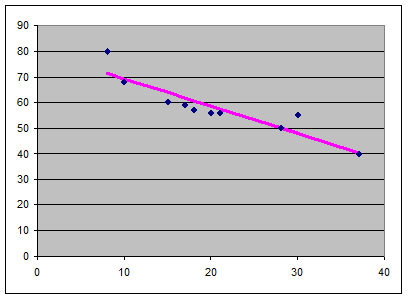
В каждом из наблюдений величину случайной компоненты можно определить как разность между фактическим значением результата и рассчитанным по уравнению регрессии:

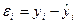Если на графике все точки совпадут с линией регрессии, то между результативным признаком у и фактором х существует функциональная зависимость, и выполняется равенство для каждого наблюдения i=1,2,…,n.

Данные, которые описывают экономические процессы, не могут иметь строгую функциональную зависимость, поскольку на результативный признак в экономике влияет большое количество факторов и случайных процессов, и все они не могут быть учтены в модели.

В парной регрессии выбор вида математической функции может быть осуществлен с помощью следующих методов:

- графического (с помощью построения поля корреляции и подбора функции, график которой проходит через большее количество точек или как можно ближе к ним);

- аналитического (исходя из экономической теории изучаемой взаимосвязи и опыта подобных предыдущих исследований);

- экспериментального (посредством перебора нескольких функций, построения нескольких уравнений регрессии и выбора того уравнения, при котором остаточная дисперсия минимальна).

После того как выбран вид уравнения регрессии (прямая линия, парабола, гипербола и т.д.) находят значения параметров модели, для линейной регрессии – это а₀ и а₁. Для этого используют метод наименьших квадратов. В основу этого метода положена идея минимизации суммы квадратов отклонений фактических значений у от их выравненных (теоретических) значений , т.е.

где у_i – фактические значения результативного признака;

– теоретические значения результативного признака, найденные по уравнению регрессии.

Если регрессия линейная , то

Рассматривая сумму S в качестве функции параметров а₀ и а₁(значения х_i и у_i в функции S являются постоянными величинами), определяют частные производные по а₀ и а₁ и приравнивают их к нулю, поскольку в точке экстремума производная функции равна нулю:

Так, если связь между признаками линейная, то система уравнений для нахождения параметров уравнения регрессии примет вид:

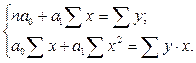
После решения системы относительно а₀ и а₁ находят уравнение регрессии .

Если связь между признаками у и х описывается уравнением параболы , то система нормальных уравнений примет вид:

Если связь описывается уравнением гиперболы , система нормальных уравнений следующая:

Вернемся к парной линейной регрессии. Решая систему уравнений относительно а и b, находят значения указанных параметров. Можно также воспользоваться следующими формулами для определения параметров а и b:

и .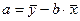

В Excel параметры а и b можно вычислить с помощью функции =ЛИНЕЙН, задав известные значения у и значения х.

Правильность расчетов параметров уравнения регрессии может быть проверена с помощью сравнения сумм:

После определения параметров уравнения регрессии а и b записывают уравнение в окончательном виде, например .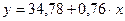

В уравнении линейной регрессии параметр а (свободный член) с математической точки зрения определяет среднее значение у, которое складывается под влиянием всех факторов, кроме х . С экономической точки зрения параметр а чаще всего не интерпретируется, поскольку чаще всего значение признака х не может быть равно нулю.

Параметр b (коэффициент при х) определяет, на сколько в среднем изменится у при изменении факторного признака на единицу.

Чем больше величина коэффициента регрессии b, тем значительнее влияние данного факторного признака на моделируемый результативный.

Знак коэффициента регрессии говорит о характере влияния фактора на результативный признак.

Экономическая интерпретация параметров линейного уравнения регрессии дополняется расчетом коэффициента эластичности:

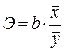Этот коэффициент показывает, на сколько процентов в среднем изменится у при изменении фактора х на 1%.