Качественная оценка связи между признаками

Значение	Характер связи
	Практически отсутствует
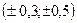
	Слабая
	Умеренная
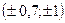
	Сильная

 

Коэффициенты корреляции как статистические величины подвергаются оценке на достоверность. Это объясняется тем, что любая совокупность наблюдений представляет собой некую выборку, следовательно, значение любого показателя, вычисленное на основе выборки, не может рассматриваться как истинное, а является только более или менее точной его оценкой. В связи с этим возникает необходимость проверки существенности (значимости) показателей.

Для оценки значимости коэффициента корреляции используют t-критерий Стьюдента:

,

где k – число факторных признаков, включенных в модель.

Соответственно для парной регрессии при k=1 t-критерий Стьюдента равен:

.

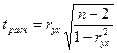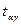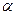Расчетное значение t-критерия Стьюдента t_расч необходимо сравнить с табличным значением , где - заданный уровень значимости (для экономических исследований обычно принимается 0,05); 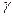- это число степеней свободы, 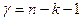. Если расчетное значение t-критерия Стьюдента t_расч больше табличного при заданном уровне значимости и числе степеней свободы, то значение коэффициента корреляции признается значимым (то есть нулевая гипотеза, утвер­ждающая равенство нулю генерального коэффициента корреляции, отвергается). И, таким образом, делается вывод о том, что между исследуемыми перемен­ными есть тесная статистическая взаимосвязь.

Зная линейный коэффициент корреляции, можно определить парный коэффициент детерминации, возведя линейный коэффициент корреляции в квадрат 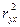. Парный коэффициент детерминации показывает, какая доля вариации переменной y учтена в модели и обусловлена влиянием на нее переменной x. Парный коэффициент детерминации определяют также по следующей формуле:

,

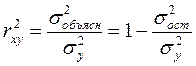где – дисперсия фактических значений результативного признака y;

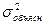– дисперсия теоретических значений результативного признака y, т.е. дисперсия y, вызванная фактором х и объясненная регрессией;

– остаточная дисперсия, т.е. дисперсия результативного признака y, вызванная влиянием других факторов, которые не включены в модель парной регрессии.

Дисперсия фактических значений результативного признака характеризует колеблемость y около их средней арифметической величины и определяется по формуле:

,

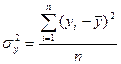где – среднее арифметическое значение y;

y_i – индивидуальные значения результативного признака y.

Дисперсия теоретических значений у или объясненная дисперсия характеризует колеблемость теоретических значений y около их средней арифметической величины и определяется по формуле:

,

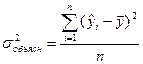где 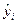– теоретические значения результативного признака, т.е. значения, полученные по уравнению регрессии.

Остаточная дисперсия характеризует колеблемость фактических значений у около их теоретических значений и определяется по формуле:

.

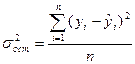Согласно правилу сложения дисперсий выполняется равенство:

.

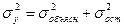Таким образом, парный коэффициент детерминации показывает, какова доля вариации, обусловленная влиянием фактора х, в общей вариации результативного признака у. Коэффициент детерминации изменяется в пределах от нуля до единицы включительно. Чем больше коэффициент детерминации, тем больше факторный признак х определяет результативный признак у.