Минимизация неполных автоматов

 

Эта задача сводится к поиску квазиэквивалентного автомата, который имеет наименьшее число состояний, и решается следующим образом.

Сначала на множестве состояний S = {s₁, s₂, ..., s_r} исходного автомата определяется отношение совместимости. Состояния s_i и s_j называют совместимыми, если любая допустимая для этих состояний входная последовательность не порождает различных заключительных выходов при начальных состояниях s_i и s_j автомата. Отношение совместимости рефлексивно и симметрично, однако оно не обязательно транзитивно. Отсюда следует, что совместимость является отношением толерантности. Все совместимые между собой состояния объединяются в классы толерантности S^'₀, S^'₁, ..., S^'_w, которые образуют некоторое покрытие множества состояний (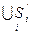=S).

Для определения совместимых состояний можно воспользоваться методом, аналогичным изложенному для полных автоматов. Исходная таблица содержит пары таких состояний, при которых для любого допустимого символа отсутствуют различные выходы. Клетки, соответствующие запрещенным входам для данной пары состояний, заполняются прочерком и при исключении пар, как это описывалось ранее, не учитываются. Так, для автомата, заданного табл. 12, имеем:

Таблица 13

x(n) Пары
0,1	-	-
0,2	1,3	-
0,3	1,5	-
0,4	1,5	-
0,5	-	-
1,4	-	4,5
1,5	-	-
2,3	3,5	1,5
2,4	3,5	1,5
2,5	-	-
3,4	5,5	5,5
3,5	-	-
4,5	-	-

 

Отмеченная на первом шаге пара {0, 2} является единственной несовместимой парой в таблице, так как она не содержится ни в каких других строках. Следовательно, всенеотмеченные пары являются совместимыми.

Пусть S₁, S₂, …, S_n – множества состояний автомата М такие, что каждое состояние автомата М включено, по крайней мере, в одно множество S_i. Множество множеств S₁, S₂, …, S_n называется группировкой; n называется мощностью группировки. Два состояния, которые находятся вместе, по крайней мере, в одном множестве S_i, составляют сопряженную пару; пара состояний, которая не является сопряженной, называется разобщеннои парой. Группировка называется правильной, если она удовлетворяет двум следующим условиям:

1) реакции автомата М, находящегося в состоянии s_i или s_j, где s_i и s_j составляют любую сопряженную пару, на любой входной символ x_i, допустимый для s_i и s_j одинаковы;

2) состояния, в которые переходит автомат из состояний s_i и s_j под воздействием x_i, одинаковы или составляют сопряженную пару.

Введем определение совместимого множества (С-множества). С-множеством автомата M будем называть множество состояний автомата M, которое удовлетворяет следующим условиям:

1) каждая пара состояний из С-множества совместима;

2) это множество не является подмножеством другого С-множества, содержащего большее число состояний.

Процедура получения всех С-множеств из совместимых пар состоит в следующем.

Даны все совместимые пары автомата М; требуется определить все С-множества автомата М.

1. Пусть первый перечень множеств состояний состоит из всех совместимых пар автомата М и из отдельных состояний, не при- надлежащих ни к одной из совместимых пар. Полагаем k=2.

2. Для каждого множества состояний {, , ..., 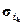}, содержащихся в (k-1)-м перечне, выполняем следующие операции. Определяем l состояний автомата М, скажем , , 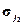..., , таких, что 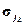(d = 1, 2, ..., l) не включено в данное множество, и таких, что каждое 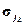образует совместимую пару с каждым состоянием из этого множества. 3аменяем множество {, , ..., 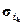} l множествами {, , ..., , 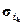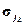}, d = 1, 2, ..., l. Если l =0, то заменим множество {, , ..., 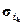} самим собой.

3. Исключаем из нового перечня множеств все одинаковые множества, оставляя по одному представителю от каждой группы одинаковых множеств, и все множества, являющиеся подмножествами других множеств. Пусть полученный таким образом перечень будет k-м перечнем.

4. Если k-й перечень отличается от (k – 1)-го перечня, то увеличиваем k на единицу и возвращаемся к пункту 2. Если k-й перечень совпадает с (k – 1)-м, то он является перечнем всех С-множеств автомата М.

Выполнение данного алгоритма облегчается построением матрицы совместимости, обозначаемой [С_M], элемент (i, j) которой равен 1, если {s_i, s_j} или {s_j, s_i} – совместимые пары состояний, и 0 в противном случае. По построению, если в каждой строке , , ..., 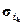содержится 1 в каком-либо данном столбце 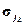, то 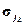образует совместимые пары с каждым состоянием из множества {, , ..., 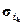}. Следовательно, если {, , ..., 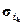} – множество в (k – 1)-м перечне и если строки , , ..., 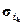матрицы совмещений содержат единицу в столбце 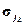, то {, , ..., 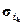} должно быть заменено множеством , , ..., ,}.

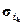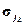В качестве примера рассмотрим автомат приведенный в начале данного раздела. На основании таблицы пар совместимости построим матрицу совместимости в следующем виде:

 

[CM] =

 

Составляем первый список:

{0,1}, {0,3}, {0,4}, {0,5}, {1,4}, {1,5}, {2,3}, {2,4}, {2,5}, {3,4}, {3,5}, {4,5}.

Из матрицы совместимости и первого списка можно найти второй список:

{0,1,4}, {0,1,5}, {0,3,4}, {0,3,5}, {0,4,5}, {1,4,5}, {2,3,4}, {2,4,5}, {3,4,5}.

Например, обе строки 0 и 1 содержат единицы в столбцах 4 и 5; поэтому множество {0,1} первого списка заменяется множествами {0,1,4} и {0,1,5}. Из матрицы совместимости и второго списка можно найти третий список:

S₁ ={0,1,4,5}, S₂ ={0,3,4,5}, S₃ ={2,3,4,5}.

Так как этот список такой же, как четвертый, то он содержит все С-множества исходного автомата.

Минимальная форма автомата M соответствует наименьшей правильной группировке, построенной из перечисленных С-множеств или из подмножеств этих С-множеств. Так как каждая группировка должна содержать все шесть состояний, минимальная правильная группировка должна иметь мощность 2 или больше.

Так, в нашем примере при воздействии 0 классы S₁ и S₂ переходят в {1, 5}, а S₃ – в {3, 5}; при воздействии 1 класс S₁ переходит в {4, 5}, S₂ – в {5} и S₃ – в {1, 5}. Следовательно, исходный автомат можно представить квазиэквивалентным ему автоматом, в котором классам совместимости S₁, S₂,..., S_w соответствуют состояния s₁, s₂, ..., s_w . Однако такой автомат не всегда будет минимальным. Для получения минимальной формы автомата необходимо отобрать наименьшее число таких классов совместимости, которые образуют покрытие множества состояний S и в то же время включают множества состояний, следующих за состояниями каждого класса при всех незапрещенных воздействиях. Для рассматриваемого примера этим требованиям удовлетворяют классы S₁ и S₂, так как S₁ 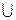S₂ = S, и все множества последующих состояний {1, 5}, {3, 5}, {4, 5} и {5} являются подмножествами S₁ и S₂, т.е. образуют наименьшую правильную группировку. Соответствующая минимальная форма показана на рис. 7, где состояния 0и 1 соответствуют классам S₁ и S₂.

 

 

 

Рис. 7