Электрическая цепь переменного тока с емкостным элементом

 

Пусть в электрической цепи (рис. 5.13) емкостной элемент (конденсатор) C подключен к источнику напряжения, изменяющемуся по синусоидальному закону:

. (5.19)

 

C i

 

U_C

 

Рис.5.13

 

Для упрощения начальная фаза тока принята равной нулю (). Из-за переменного характера напряжения на полюсах конденсатора, между его обкладками возбуждается электрическое поле, изменяющееся во времени по синусоидальному закону. Под воздействием сил поля ток в цепи изменяется пропорционально скорости изменения заряда пластин конденсатора: .

Поскольку заряд , то выражение для тока емкостного элемента:

. (5.20)

Следовательно, мгновенное значение тока через емкостной элемент опережает приложенное к нему напряжение на . Векторная и угловая диаграммы тока и напряжения на емкостном элементе приведены на рис. 5.14.

 

U, i

Um

I_m I_m

 

π/2 U_m π

-π/2 0 π/2 ωt

U

i

 

Рис.5.14

 

Преобразуем (4.20), выразив мгновенный ток 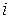через его амплитудное значение :

, (5.21)

где , а – емкостное сопротивление конденсатора.

Размерность емкостного сопротивления – (Ом). Поделив в (5.20) амплитудные значения тока и напряжения на , получим закон Ома для действующих значений:

. (5.22)