Дифференциальные уравнения ламинарного пограничного слоя.
Перейдем теперь к выводу уравнений жидкости в пограничном слое. Пусть характерный размер обтекаемого тела (например, длина) равен L. Тогда в свете сказанного логично положить  . Для анализа удобно выбрать естественную систему координат, в которой одна координатная линия повторяет очертание тела. Такой выбор особенно ценен при конечно-разностном методе решения задачи, поскольку позволяет точно удовлетворять граничным условиям на стенке. Однако на первом этапе анализа систему координат можно принять прямолинейной декартовой системой (х, у), полагая радиусы кривизны профиля достаточно большими по сравнению с толщиной пограничного слоя
. Для анализа удобно выбрать естественную систему координат, в которой одна координатная линия повторяет очертание тела. Такой выбор особенно ценен при конечно-разностном методе решения задачи, поскольку позволяет точно удовлетворять граничным условиям на стенке. Однако на первом этапе анализа систему координат можно принять прямолинейной декартовой системой (х, у), полагая радиусы кривизны профиля достаточно большими по сравнению с толщиной пограничного слоя  .
.
В случае двухмерного течения полная система уравнений Навье - Стокса имеет вид
 (2.118)
(2.118)
Выберем характерные масштабы переменных величин, содержащихся в системе. Пусть L, U — масштабы продольной координаты X и компоненты скорости u; 
 - масштабы поперечной координаты Y и компоненты скорости
- масштабы поперечной координаты Y и компоненты скорости  , Р - масштаб давления,
, Р - масштаб давления,  - масштаб времени. Произведем оценку членов, входящих в систему. Равенство по порядку величин будем обозначать буквой О.
- масштаб времени. Произведем оценку членов, входящих в систему. Равенство по порядку величин будем обозначать буквой О.
Из последнего уравнения системы (уравнения неразрывности) следует, что производные  и
и  имеют одинаковый порядок. Так как
имеют одинаковый порядок. Так как
 ,
,  ,
,
то

или
 . (2.119)
. (2.119)
Из первого уравнения системы вытекают оценки:
 ,
,  ,
,  ;
;
 ,
,  ,
,  .
.
Нетрудно заключить, что
 ,
,
т. е. членом  можно пренебречь.
можно пренебречь.
Если принять, что масштабы давления и времени равны
 ,
,  ,
,
то все члены, кроме вязкого, будут иметь порядок  . Но этот порядок должен быть внутри пограничного слоя равен порядку вязкого члена. Это означает, что
. Но этот порядок должен быть внутри пограничного слоя равен порядку вязкого члена. Это означает, что
 или
или  ,
,
где  .
.
Таким образом, основной малый параметр  обратно пропорционален корню квадратному из числа Рейнольдса:
обратно пропорционален корню квадратному из числа Рейнольдса:
 . (2.120)
. (2.120)
Второе уравнение системы приводит к следующим оценкам:
 ;
;
 ,
,  ,
,  ;
;
 .
.
Последний член имеет самый низкий порядок и может быть опущен. Остальные члены имеют одинаковый порядком  . Отсюда следует, что такой же порядок должен иметь и член, содержащий производную от давления, т.е. должно быть
. Отсюда следует, что такой же порядок должен иметь и член, содержащий производную от давления, т.е. должно быть
 . (2.121)
. (2.121)
Как видим, можно заключить
 .
.
Иными словами, оценка членов второго уравнения системы приводит к выводу, что давление поперек пограничного слоя остается постоянным, потому что
 , (2.122)
, (2.122)
и равным давлению на внешней границе пограничного слоя.
Собирая полученные результаты, запишем систему дифференциальных уравнений ламинарного пограничного слоя (уравнения Прандтля):
 (2.123)
(2.123)
Заметим, что из условия сшивания вязкого течения в пограничном слое с потенциальным внешним течением вытекает, что слагаемое  может быть определено из решения потенциальной задачи, например, с помощью интеграла Коши — Лагранжа. Тогда
может быть определено из решения потенциальной задачи, например, с помощью интеграла Коши — Лагранжа. Тогда
 , (2.124)
, (2.124)
где  - скорость на поверхности твердого тела при потенциальном обтекании, равная скорости на внешней границе пограничного слоя.
- скорость на поверхности твердого тела при потенциальном обтекании, равная скорости на внешней границе пограничного слоя.
Для получения единственного решения системы (2.123) необходимо сформулировать начальные и граничные условия. Начальное условие записывается в виде:
при t = 0: u = u (0, x, y). (2.125)
На твердой стенке (внутренней границе) должно выполняться граничное условие прилипания:
при y = 0: u = 0,  . (2.126)
. (2.126)
На границе слева:
при  :
:  . (2.127)
. (2.127)
На внешней границе можно ставить граничное условие либо при  , и тогда говорят об асимптотическом пограничном слое, либо при
, и тогда говорят об асимптотическом пограничном слое, либо при  , тогда говорят о слое конечной толщины. В качестве примера запишем граничное условие для асимптотического пограничного слоя:
, тогда говорят о слое конечной толщины. В качестве примера запишем граничное условие для асимптотического пограничного слоя:
при  :
:  . (2.128)
. (2.128)
Можно ввести в рассмотрение функцию тока как:
 ,
,  ,
,
что позволяет получить вместо системы (2.123) одно уравнение
 (2.129)
(2.129)
с граничными условиями:
 при
при 
 ;
;
при 
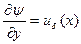 ; (2.130)
; (2.130)
при 
 .
.
При решении конкретных задач форма записи уравнений ламинарного пограничного слоя выбирается наиболее подходящей для исследуемого случая. Одним из эффективных методов преобразования уравнений к удобному виду является замена переменных, и, в частности, использование переменных Прандтля — Мизеса.
В заключение отметим, что теория ламинарного пограничного слоя приложима к течению в струях и следах.