Свободное падение
Особый интерес с практической точки зрения представляет свободное движение тела в поле тяжести Земли – свободное падение. Свободным падением называется движение тела в состоянии, когда на него кроме силы тяжести больше ничего не действует. В XVII веке Галилей экспериментально показал, что свободное падение тел является равноускоренным движением. Более того, ускорение, с которым движутся свободно падающие тела, имеет одно и то же значение, одинаковое для всех тел и приблизительно равное 9,8 м/с2. Направлено это ускорение тоже для всех тел одинаково – вертикально вниз. Это ускорение называется ускорением свободного падения и обозначается – g (g = 9,8 м/с2).
Естественно о свободном падении можно говорить только в случае, если можно пренебречь сопротивлением воздуха. Абсолютно строго в условиях Земли это никогда не выполняется. Однако, если движущееся тело имеет достаточно большую плотность и его скорость не очень велика, то влиянием сопротивления воздуха в первом приближении можно пренебречь. Поэтому во всех задачах, связанных со свободным падением, сопротивлением воздуха пренебрегается.
Рассмотрим теперь некоторые конкретные движения, относящиеся к свободному падению.
1. Свободное падение без начальной скорости.
 Пусть тело свободно падает без начальной скорости из точки, находящейся на высоте Н над поверхностью земли. Направим координатную ось Y вертикально вниз. Пусть начало координат совпадает с точкой начала падения. Движение тела является равноускоренным. Поэтому можно записать зависимость скорости и координаты тела от времени в виде:
Пусть тело свободно падает без начальной скорости из точки, находящейся на высоте Н над поверхностью земли. Направим координатную ось Y вертикально вниз. Пусть начало координат совпадает с точкой начала падения. Движение тела является равноускоренным. Поэтому можно записать зависимость скорости и координаты тела от времени в виде: 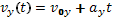 ;
; 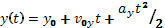 .
.
Так как начальная скорость равна нулю, то v0y = 0. Так как Начало координатной оси находится в точке начала движения, то y0 = 0. Так как координатная ось направлена вниз и ускорение свободного падения равно g и тоже направлено вертикально вниз, то ay = g. Значит, для нашего конкретного случая получаются такие уравнения:  ;
; 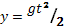 .
.
В момент падения тела на землю, его координата станет равна Н. Значит, для момента падения можно написать 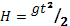 . Откуда сразу получаем время падения тела:
. Откуда сразу получаем время падения тела:
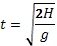
Подставив это время в зависимость скорости тела от времени, получаем скорость тела в момент падения:
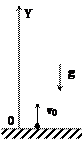
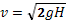
2. Движение тела, брошенного вертикально вверх.
Пусть тело бросили с поверхности земли с начальной скоростью v0, направленной вертикально вверх. Направим ось Y вертикально вверх с поверхности земли. Так как движение равноускоренное, то можно написать: 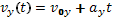 ;
; 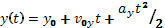 . Для нашего конкретного случая: y0 = 0; v0y = v0; ay = −g.
. Для нашего конкретного случая: y0 = 0; v0y = v0; ay = −g.
Получаются такие исходные уравнения: 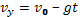 ;
;  . Из опыта мы знаем, что в случае такого движения тело сначала будет подниматься вверх, затем в высшей точке своего движения на мгновение остановится и начнет падать вниз. Значит, в момент подъема тела на максимальную высоту его скорость станет равна нулю. То есть для этого момента времени можно записать: . Отсюда сразу получаем время движения тела до точки максимального подъема:
. Из опыта мы знаем, что в случае такого движения тело сначала будет подниматься вверх, затем в высшей точке своего движения на мгновение остановится и начнет падать вниз. Значит, в момент подъема тела на максимальную высоту его скорость станет равна нулю. То есть для этого момента времени можно записать: . Отсюда сразу получаем время движения тела до точки максимального подъема:  . Координата y в нашем случае автоматически является высотой поднятия тела. Если мы подставим этот момент времени в зависимость координаты от времени, то получим координату тела в момент достижения максимальной высоты, то есть, как раз максимальную высоту подъема тела:
. Координата y в нашем случае автоматически является высотой поднятия тела. Если мы подставим этот момент времени в зависимость координаты от времени, то получим координату тела в момент достижения максимальной высоты, то есть, как раз максимальную высоту подъема тела:
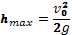
В момент падения тела на землю его координата станет равна нулю. То есть для этого момента можно написать: . Решая это уравнение относительно времени t, получаем два корня: t1 = 0; t2 = 2v0/g. Формально это свидетельствует о том, что в процессе движения координата тела два раза была равна нулю. Очевидно, что первый корень соответствует моменту бросания тела, а второй – моменту падения. Значит время, через которое брошенное тело упадет на землю, равно:
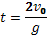
Кстати заметим, что это время ровно в 2 раза больше времени подъема тела до максимальной высоты. Это значит: сколько времени брошенное тело поднимается вверх, столько же оно падает обратно вниз. Если мы теперь найденное время падения тела на землю подставим в зависимость скорости от времени, то получим скорость падения тела. Она равна: 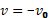 . То есть мы получили, что тело упадет обратно на землю с той же скоростью, с какой его бросили. Знак минус означает, что проекция скорости падения тела на ось Y отрицательна, то есть она направлена вертикально вниз.
. То есть мы получили, что тело упадет обратно на землю с той же скоростью, с какой его бросили. Знак минус означает, что проекция скорости падения тела на ось Y отрицательна, то есть она направлена вертикально вниз.
3. Движение тела, брошенного горизонтально.
Пусть тело брошено горизонтально с начальной скоростью v0 с высоты Н.
 В данном случае движение тела будет также равноускоренным, но не прямолинейным. Траектория движения тела будет представлять собой некую кривую линию. А это значит, что для описания движения тела нам будет недостаточно одной координатной оси. Однако, как показывает опыт, траектория такого движения находится в одной плоскости, то есть нам достаточно системы координат из двух осей. Выберем систему координат из двух осей X и Y. Причем начало координат поместим в точку бросания, ось Х направим горизонтально в сторону бросания тела, а ось Y направим вертикально вниз. Так как движение является равноускоренным, то можно написать:
В данном случае движение тела будет также равноускоренным, но не прямолинейным. Траектория движения тела будет представлять собой некую кривую линию. А это значит, что для описания движения тела нам будет недостаточно одной координатной оси. Однако, как показывает опыт, траектория такого движения находится в одной плоскости, то есть нам достаточно системы координат из двух осей. Выберем систему координат из двух осей X и Y. Причем начало координат поместим в точку бросания, ось Х направим горизонтально в сторону бросания тела, а ось Y направим вертикально вниз. Так как движение является равноускоренным, то можно написать:
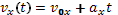 ;
; 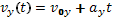
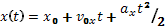 ;
;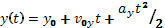
Для нашего случая: x0 = y0 = 0; v0x = v0; v0y = 0; ax = 0; ay = g. Таким образом, получается следующая система исходных уравнений:
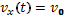
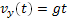
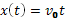
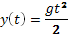
В момент падения тела на землю его координата y будет равна Н. То есть для этого момента можно написать: 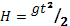 . Откуда сразу получаем время падения тела:
. Откуда сразу получаем время падения тела:
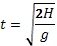
Расстояние, которое пролетит тело по горизонтали до места падения равно х-овой координате в момент падения:
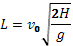
Проекции скорости тела в момент падения равны:
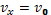 ;
; 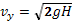
Поэтому полная скорость в момент падения равна:

Угол α между вектором скорости и горизонтальной осью Х в момент падения определяется из условия:
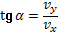
4. Движение тела, брошенного под углом к горизонту вверх.
Пусть тело брошено с начальной скоростью v0 под углом α к горизонту с поверхности земли и падает на поверхность земли.
В данном случае движение тела также является равноускоренным, но не прямолинейным. Поэтому для описания этого движения также требуется система координат из двух осей Х и Y. Совместим начало координат с точкой бросания, ось Х направим горизонтально в сторону бросания, а ось Y направим вертикально вверх. Так как движение является равноускоренным, то можно написать:
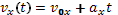 ;
; 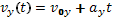
 |
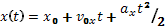 ;
;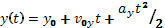
Для нашего случая: x0 = y0 = 0; 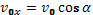 ;
; 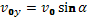 ; ax = 0; ay = −g. Таким образом, получается следующая система исходных уравнений:
; ax = 0; ay = −g. Таким образом, получается следующая система исходных уравнений:




В момент падения на землю координата y тела равна нулю. Приравнивая зависимость y(t) к нулю получаем квадратное уравнение относительно t, корни которого t1 = 0,  . Первый корень, очевидно, соответствует моменту бросания тела, а второй – моменту падения. Значит время полета тела равно:
. Первый корень, очевидно, соответствует моменту бросания тела, а второй – моменту падения. Значит время полета тела равно:

Дальность полета тела – расстояние от точки бросания до точки падения равна координате х в момент падения тела на землю. Подставляя в зависимость x(t) момент времени t2, получаем дальность полета:

Траектория движения тела представляет собой некую кривую линию, имеющую максимум подъема. Вектор скорости тела в любой точке направлен по касательной к траектории. А значит, в точке максимального подъема вектор скорости тела направлен горизонтально и его проекция на ось Y равна нулю. Приравняв зависимость vy(t) к нулю и выразив из полученного уравнения t, получим момент времени, в который тело проходило точку максимального подъема:

Это время ровно вдвое меньше времени полета. Это значит, что время подъема тела до точки максимального подъема равно времени обратного падения на землю. Координата y в нашем случае соответствует высоте подъема тела. Значит, подставив момент времени t’ в зависимость y(t), мы получим максимальную высоту подъема тела:

Наконец, выясним, что представляет собой траектория полета тела. Для этого выразим время из зависимости x(t):  и подставим его в зависимость y(t). Получаем уравнение траектории движения тела:
и подставим его в зависимость y(t). Получаем уравнение траектории движения тела:

Мы получили квадратичную зависимость y(x). Причем коэффициент при х2 отрицательный. Графиком такой зависимости является парабола с ветвями, направленными вниз. Значит траекторией движения тела, брошенного под углом к горизонту, является парабола с ветвями, направленными вниз.
Бросая тело с одинаковой начальной скоростью, но под разными углами к горизонту, дальность полета будет получаться разной. А под каким углом надо бросить тело, чтобы оно улетело как можно дальше? Из формулы для дальности полета видно, что дальность будет максимальной, когда  примет максимальное значение. Но максимальное значение синуса равно единице и реализуется это значение для угла 90°. Значит дальность полета будет максимальной когда 2α = 90°, то есть α = 45° и равна эта максимальная дальность полета:
примет максимальное значение. Но максимальное значение синуса равно единице и реализуется это значение для угла 90°. Значит дальность полета будет максимальной когда 2α = 90°, то есть α = 45° и равна эта максимальная дальность полета:  .
.
Рассмотрим следующую задачу. Мальчик, бросая мяч с некоторой начальной скоростью, может бросить его на максимальное расстояние 40 м. Под каким углом к горизонту мальчик должен бросить мяч с той же скоростью, чтобы он упал на расстоянии 20 м от точки бросания? Рост мальчика не учитывать.
Решение. Максимальная дальность полета реализуется для угла бросания 45° и равна  . Для любого другого угла бросания α можно написать:
. Для любого другого угла бросания α можно написать:  . Значит, для нашего случая получаем:
. Значит, для нашего случая получаем:  . Далее надо найти угол, синус которого равен 0,5. Однако следует заметить, что угол бросания α может изменяться от 0 до 90°, а значит угол 2α может изменяться от 0 до 180°. В диапазоне от 0 до 180° имеется два угла, синус которых равен 0,5 – это 30° и 150°. А значит имеется два угла бросания, при которых мяч улетит на 20 м: α1 = 15° и α2 = 75°.
. Далее надо найти угол, синус которого равен 0,5. Однако следует заметить, что угол бросания α может изменяться от 0 до 90°, а значит угол 2α может изменяться от 0 до 180°. В диапазоне от 0 до 180° имеется два угла, синус которых равен 0,5 – это 30° и 150°. А значит имеется два угла бросания, при которых мяч улетит на 20 м: α1 = 15° и α2 = 75°.
Дело в том, что это не единственная дальность, которая обеспечивается при двух различных углах бросания. Для любого значения синуса в диапазоне от 0 до 180° существует два угла: 2α и 180° - 2α. А значит любая дальность полета при заданной скорости бросания обеспечивается при двух углах бросания: α и 90° - α. В артиллерии эти две траектории снаряда имеют названия. Траектория, соответствующая углу α < 45° называется настильной, а траектория, соответствующая углу 90° - α называется навесной.