Равновесие жидкости в поле силы тяжести и силы инерции (относительный покой)

Пусть жидкость налита в сосуд, вращающийся с постоянной угловой скоростьюω вокруг вертикальной оси.

 

 

 

Благодаря силам трения, возникающим при движении стенки вращающегося сосуда, будут увлекать за собой жидкость и по истечении некоторого времени вся жидкость будет вращаться вместе с сосудом с той же угловой скоростью ω, находясь по отношению к стенкам в покое.

В данном случае объемная сила F, действующая на единицу массы жидкости, состоят из двух сил: силы тяжести g и центробежной силы инерции ω²r.

Тогда проекции объемной силы на оси координат будут равны:

X=ω²rcos£

Y=ω²rsin£

Z= -g

Имея в виду, что r cos £=x, r sin £= y

Будем иметь:

X=ω²x,

Y=ω²y,

Z=-g.

Подставив значения ускорения в уравнение Эйлера, получим

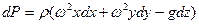
Проинтегрировав это уравнение, получим

Зная, что x²+y²=r², получим

Р=ρ ω²r²\2 – γz+ C

Константу С находим из условия r=0, z =z₀'

P₀=γz₀^' + С, откуда С=Р₀+γz₀^'_, где Р₀=Р_ат=0

Тогда

Р= ρ ω² r²\2 – γ(z – z₀)

 

 

Найдем уравнение свободной поверхности.

В этом случае Р=Р₀=Р_атм

 

γ( Z₀-Z₀^') =ρ ω² r²|2

 

 

(Z₀-Z₀^')=h= ω²r²\2g

 

Из уравнения следует, что свободная поверхность жидкости, представляет собой параболоид вращения.