Оптимизация портфеля ценных бумаг предприятия

Данный раздел посвящен выбору оптимизации структуры портфеля ценных бумаг предприятия. Последовательно рассмотрены модели оптимизации фондового портфеля: Марковица и Шарпа.

Основными характеристиками любой ценной бумаги являются – ее доходность и показатель риска. Как правило, ценные бумаги, обладающие низким показателем риска, дают небольшую доходность, а ценные бумаги, которые могут дать большой доход, имеют значительные показатели риска.

Риск принято разделять на рыночный– единый для всех ценных бумаг, которого невозможно избежать, и индивидуальный– присущий конкретной ценной бумаге. Размещая денежные средства в различные ценные бумаги, т.е. формируя портфель ценных бумаг, можно снизить индивидуальный риск: если по одним ценным бумагам будет низкий доход или убыток, то другие это компенсируют своей более высокой доходностью. Чем больше ценных бумаг содержится в портфеле, т. е. чем более он диверсифицирован, тем меньше индивидуальный риск.

Каждое предприятие, желающее разместить свободные средства на фондовом рынке, имеет свою шкалу оценки риска и доходности. Высокая доходность для одного предприятия может показаться низкой для другого. Одни предпочитают низкий риск с низкой доходностью, а другие – согласны на больший риск с большей ожидаемой доходностью.

Целью оптимизации портфеля ценных бумаг является формирования такого портфеля ценных бумаг, который бы соответствовал требованиям предприятия, как по доходности, так и по рискованности, что достигается путем увеличения количества ценных бумаг в портфеле.

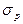Сформулируем задачу оптимизации. Пусть доходность портфеля из N ценных бумаг и его показатель риска определяются следующими функциями:

;

где — процентная доля ценной бумаги в портфеле;

— некоторая характеристика риска данной ценной бумаги, обычно это среднее квадратичное отклонение доходности ценной бумаги;

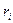— доходность ценной бумаги.

Содержание каждой функции определяется в дальнейшем при построении модели доходности и риска.

При решении задачи необходимо учесть следующие естественные ограничения:

— сумма долей всех акций (в процентах) составляет 100%:

;

— количество акций не может быть отрицательным:

.

Решением задачи является некоторая целевая структура портфеля, представленная набором значений (). Идеальная постановка задачи оптимизации портфеля — получить максимальную доходность при минимальном риске:

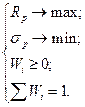
Но такая задача некорректна, т. е. не имеет однозначного решения. Идеальный результат не достижим, как и все идеальное.

Выходом из положения является введение критериальных ограничений.

Первый вариант — задаться некоторой максимально допустимой величиной риска 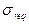. Тогда задача оптимизации сводится к выбору такой структуры портфеля, при которой риск портфеля не превышает заданного значения, а доходность портфеля является максимальной. Такая задача будет в дальнейшем называться прямой задачей:

 

Второй вариант — задаться некоторой минимально приемлемой величиной доходности . В этом случае задача оптимизации сводится к выбору такой структуры портфеля, доходность которого выше либо равна заданному значению, а риск минимален:

Решив прямую и обратную задачи по оптимизации портфеля из N ценных бумаг, предприятие получит данные о том, сколько и каких ценных бумаг необходимо приобрести, чтобы сформировать портфель, имеющий (по меркам предприятия) достаточно высокую доходность при приемлемом риске.

При попытке решения прямой либо обратной задач возникает вопрос, каким образом определяются характеристики портфеля (доходность и риск)? На сегодняшний день наиболее распространены две модели определения характеристик портфеля: модель Марковица и модель Шарпа. Обе модели созданы и успешно работают в условиях уже сложившихся относительно стабильных западных фондовых рынков.