Волны де Бройля
Так как электрон проявляет одновременно волновые и корпускулярные свойства, то возникла идея, что этим обладают и все остальные частицы и поэтому общие законы механическим частицам и механические волны должны совпадать.
В теории волны таким общим законом является принцип Ферма, которой позволяет описывать траектории луча из условий минимума 
Оказывается, что такой же принцип существует и в классической механике  должен быть min
должен быть min
Очевидно, что объединив свойства траектории луча и траектории частицы это одно и тоже, поэтому оба принципа должны удовлетворятся одновременно

С другой стороны скорость частицы

 групповая скорость волн.
групповая скорость волн.

Так как это равенство должно выполняться для любых E и u то коэффициенты (E,u) в левой и правой частях должны быть равны.


 постоянная Планка
постоянная Планка

Интегрируя получим

 произвольная постоянная величина
произвольная постоянная величина
Так как если частицы нет то  и
и  то очевидно, что
то очевидно, что 




Таким образом, частица с одной стороны характеризует корпускулярные характеристики E и  , а с другой стороны волновыми
, а с другой стороны волновыми  и
и  которые связаны соотношением
которые связаны соотношением
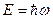


Так как 
 - длина волны Дебройля
- длина волны Дебройля
Таким образов каждая частица соответствует некоторая волновая функция.


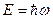
Получим волновую функция называемую волной Дебройля.