Модель с распределенными параметрами

Модели с распределенными параметрами представляют собой систему уравне­ний движения, баланса тепла и массы газовых примесей в дифференциальной форме в частных производных. Система уравнений дополняется краевыми усло­виями, в состав которых входят граничные условия и начальные условия. Реше­ние системы позволяет определить трехмерное распределение параметров мик­роклимата в объеме помещения и изменяющимися во времени. Такие модели, как правило, используются при решении исследовательских задач. Поэтому они учитывают по возможности полную постановку задачи, являются сложными и не имеют широкого распространения в инженерной практике.

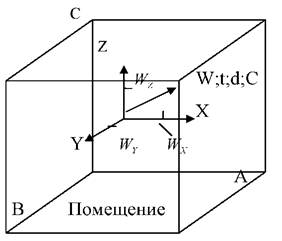Рассмотрим в несколько упрощенной постановке модель распределения в по­мещении скорости и температуры воздуха (см.рис.2.1). За основу модели принята система уравнений движения Навье-Стокса, описывающая движение потока однородной несжимаемой вязкой жидкости .

Рис.2.1. К определению модели с распределенными параметрами

Упрощение состоит в том, что воздух является сжимаемой жидкостью и в рассматриваемой задаче имеет газообразные или аэрозольные (пыль) примеси загрязняющих веществ. Однако, несущественное изменение давления в помещении позволяет считать воздух несжимаемым, а малые концентрации вредных веществ в общем объеме помещения позволяет считать воздушную среду однородной.

Система включает в себя уравнения проекции вектора скорости на оси ординат

 

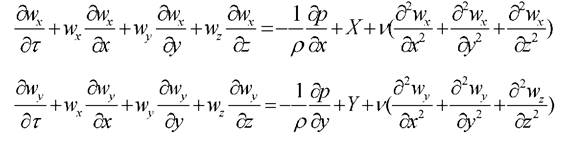(2.1)

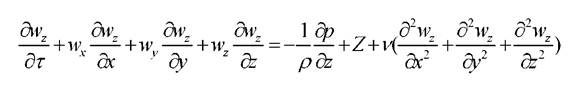
Система уравнений дополняется уравнением сплошности потока

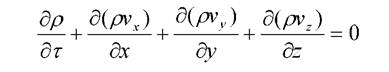(2.2)

 

Уравнение распределения температуры в движущемся потоке и уравнение состояния

 

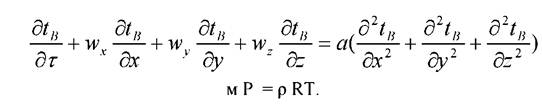(2.3)

 

Уравнение распространения примеси в воздухе потока

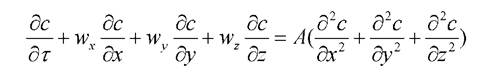(2.4)

 

В уравнениях (2.1) - (2.4) приняты следующие обозначения:

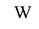-скорость движения воздуха, м/с;

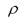-плотность воздуха, кг/м3;

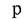-давление, Па;

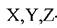-проекция плотности массовых сил на оси, Па;

-кинематическая вязкость воздуха, м2/с;

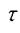-время, с;

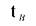-температура воздуха, град;

 

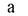-коэффициент температуропроводности воздуха, м2/с;

-масса воздуха, кг;

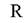-газовая постоянная, кг м/кг град;

-число Прандтля для воздуха

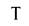-температура воздуха, ⁰K;

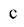-концентрация газовой примеси, мг/м3;

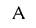-коэффициент турбулентного обмена, м2/с.

В приведенной записи системы уравнений отсутствуют члены, учитывающие молекулярную диффузию газовых примесей и турбулентность движущегося по­тока воздуха. Турбулентный поток характеризуется неупорядоченностью, которая приводит к случайному изменению во времени и пространстве мгновенных зна­чений скорости температуры, давления в потоке. Условно турбулентное движе­ние рассматривают как движение совокупности отдельных объемов жидкости, совершающих как поступательное, так и вращательное движение.

Для математического описания турбулентного движения используются раз­ные модели, в том числе метод Рейнольдса, состоящий в разделении мгновенных значений параметров на две части - среднюю и пульсационную

Граничные условия системы уравнений отображают условия теплообмена на границах, которыми являются ограждения помещения с координатами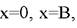

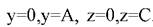. При этом имеется в виду, что на границах скорость потока

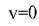
На поверхности ограждения, обращенной внутрь помещения, в любой момент времени удовлетворяется уравнение баланса тепла. В развернутом виде уравне­ние баланса имеет вид

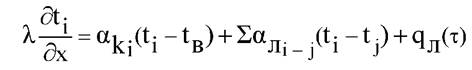. (2.5)

В толще каждого ограждения имеет место распределение температуры, описы­ваемое уравнением Фурье (для примера по координате х)

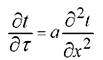. (2.6)

В уравнениях (2.5) и (2.6) принято:

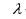- коэффициент теплопроводности материала поверхностного слоя огражде­ния, Вт/м град;

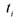- температура поверхности, град;

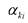- коэффициент конвективного теплообмена, Вт/м2 град;

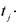- температура j -ой поверхности, град;

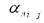-коэффициент лучистого теплообмена на внутренних поверхностях ограж­дений в помещении, Вт/м2град;

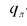- плотность лучистого теплового потока от внутренних источников, Вт/м2;

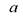- коэффициент температуропроводности материала слоя ограждения,м2/с.

Помимо граничных условий задаются начальные условия в виде численных зна­чений параметров в начальный (нулевой) момент времени.

Решение системы уравнений ведут численными методами, основанными на пе­реходе от бесконечно малых приращений координат и времени к конечным ма­лым приращениям.

Известен ряд решений подобных задач в различных отраслях знаний. В об­ласти обеспечения микроклимата помещений задача решалась с разной степенью детализации ее постановки. В полном виде численное решение было получено в Институте автоматизации и проектирования РАН А.А. Аксеновым и А.В. Гуд- зовским, которыми разработан универсальный программный комплекс Flow Vi­sion, предназначенный для решения практических задач аэродинамики и тепломассопереноса.