Методические указания

Для выполнения данного пункта краткие пояснения даны ниже.

В виде примера рассмотрим концентрический кабель с несколькими слоями диэлектрика с разными диэлектрическими проницаемостями (рис. 1.1). Вообразим цилиндрическую поверхность радиуса r и длины l, ось которой совмещена с осью кабеля. Поток смещения сквозь эту поверхность равен заряду , расположенному на отрезке / внутреннего провода кабеля, т. е. , причем

τ — линейная плотность заряда. Так как на всей поверхности ввиду симметрии D=const и вектор D нормален к поверхности, то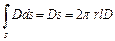

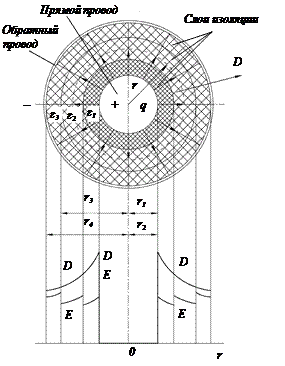
Рис. 1.1. Структура изоляции кабеля

 

Итак,

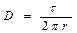
Напряженность в k-м слое изоляции равна

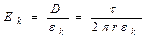
В пределах каждого слоя напряженность поля убывает с увеличением r, при переходе же к следующему слою, она изменяется скачком в связи с изменением . Этот скачок мы и можем объяснить появлением связанных зарядов на поверхности раздела двух слоев диэлектрика.

В каждом слое напряженность поля имеет максимальное значение у внутренней поверхности слоя, равное

,причем — внутренний радиус слоя. Представляется возможным при проектировании кабеля подобрать величины для всех слоев так, чтобы величины 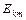отвечали допустимым значениям напряженности, соответствующим электрической прочности слоев. В частности, если допустимая максимальная напряженность поля 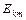во всех слоях одинакова, то следует стремиться к соблюдению условий:

Применением многослойной изоляции достигается значительное выравнивание напряженности поля вдоль радиуса, что иллюстрируется эпюрой на рис. 1.1.

Контрольные вопросы

1. Какое поле называется электростатическим?

2. Какие уравнения описывают электростатическое поле?

3. Каковы граничные условия в электростатическом поле?

4. Почему электростатическое поле называется потенциальным?

5. Когда целесообразно применять теорему Гаусса?

6. Когда целесообразно использовать уравнения Лапласа и Пуассона?

Практическая работа №2
Потенциальные и емкостные коэффициенты. Расчет частичных емкостей

Цель работы:Научиться рассчитывать потенциальные и емкостные коэффициенты, графически рассчитать напряженность электрического поля.

Условие практической работы:Трехпроводная линия (радиус проводов R=0.02 м), расположена в воздухе ( ) параллельно проводящей плоскости (земли), как показано на рис. 4.1. Координаты проводов, их потенциалы и токи заданы в табл. 2.1.

Рис. 2.1. Расчетная схема

 

Определить потенциальные и емкостные коэффициенты, частичные емкости, линейные плотности зарядов проводов, энергию электростатического поля на единицу длины, а также для точки N (координаты x, y) рассчитать потенциал j и вектор напряженности .

 

Таблица 2.1