Аналитические CНC с настройкой по характеристикам ОУ

В аналитических СНС настройку системы автоматизации на оптимальный режим можно осуществить либо за счёт изменения параметров в прямой цепи системы, либо за счёт изменения параметров в обратной цепи системы. Рассмотрим эти два случая.

1. Изменение параметров в прямой цепи системы.

Из аналитических СНС с настройкой по характеристикам ОУ наиболее часто применяется принцип самонастройки с эталонной моделью (см. п.10.1). Варьируемые параметры в CНC с эталонной моделью при стабилизации качества были определены ранее (формула (10.11)).

Определим варьируемые параметры CНC с эталонной моделью при оптимизации качества. Выберем структуру такой CНC (рис. 11.3), аналогичную структуре СНС со стабилизацией качества (см. рис. 10.1).

 

Рисунок 11.3 – Структура СНС с эталонной моделью при оптимизации качества управления,

где - варьируемые параметры

При оптимальной настройке системы сигнал рассогласования . Качество самонастройки будет зависить от сигнала рассогласования , т.е. критерий вторичной оптимизации является функцией . Существует достаточно много вариантов представления зависимости . Наиболее часто эту зависимость записывается в одной из форм:

; ; ; ; . (11.6)

Для определения варьируемых параметров воспользуемся градиентным методом (см. п.12.1), согласно которому скорость изменения параметров пропорциональна градиенту от критерия качества , т.е.

, (11.7)

где - коэффициент пропорциональности.

Поскольку критерий является функцией от сигнала рассогласования , определяемого выражением , а выход модели не зависит от варьируемых параметров , то можно записать, что

, . (11.8)

Сомножитель в выражении (11.8) при заданном критерии (11.6) является известным (например, при ). Для определения сомножителя воспользуемся передаточной функцией системы . Для этого выразим через передаточную функцию системы :

.

Тогда

, . (11.9)

Определим передаточную функцию системы для основного контура (рис. 11.4) СНС, представленного на рис. 11.3.

 

Рисунок 11.4 – Основной контур СНС с эталонной моделью

 

Как было показано в п.8.3, передаточную функцию системы, представленной на рис. 11.4, можно записать в виде (8.16):

, (11.10)

где - вектор настраиваемых параметров УУ;

- совокупность неконтролируемых параметров ОУ.

Так как 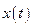не зависит от настраиваемых параметров УУ , то найдём производную , используя свойство дифференцирования :

.

Исключим передаточную функцию ОУ из последнего выражения. Для этого найдём её из (11.10):

.

Тогда

. (11.11)

. (11.12)

C учётом (11.12) выражение (11.8) примет вид:

.(11.13)

Целью самонастройки является приближение передаточной функции реальной системы к передаточной функции модели , т.е. должно выполняться условие .

Из уравнения (11.13) можно найти выражение для компонент вектора настраиваемых параметров УУ , продифференцировав (11.13) по времени .

В итоге получим

, (11.14)

где - оператор интегрирования.

С учётом (11.14) структурная схема одного канала вычислителя в составе цепи самонастройки приобретет вид, представленный на рис. 11.5.

 

 

Рисунок 11.5 - Структурная схема одного канала ЦС в СНС с оптимизацией качества

 

Всего будет таких взаимосвязанных каналов, так как каждый из них использует информацию о параметрах, определяемых остальными каналами.

2. Изменение параметров в цепи обратной связи (ОС) системы.

В ряде случаев для компенсации изменяющихся параметров ОУ используют устройства, расположенные в цепи ОС системы (рис. 11.6).

 

Рисунок 11.6 - Схема СНС с управляющим устройством в цепи обратной связи

 

Как и в предыдущем случае, для определения варьируемых параметров воспользуемся градиентным методом, согласно которому

, (11.15)

где .

Так как сомножитель можно определить из выражения для критерия вторичной оптимизации (11.6), то остановимся на определении сомножителя .

Из рис. 11.6 видно, что .

Учитывая, что 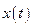не зависит от варьируемых параметров , можно записать:

, . (11.16)

Определим передаточную функцию системы :

.

Откуда следует, что

.

С учётом этого система (рис. 11.6) будет описываться передаточной функцией

. (11.17)

Найдём производную :

. (11.18)

Выразим передаточную функцию ОУ через передаточную функцию системы .

Из (11.17) видно, что

. (11.19)

После подстановки (11.19) в (11.18) имеем:

.

С учётом выполненных преобразований выражение (11.15) примет следующий вид:

,(11.20)

где .

Из рассуждений, приведенных для случая изменения параметров в прямой цепи, положим . Тогда из (11.20) получается выражение для компонент вектора настраиваемых параметров УУ :

, (11.21)

где - оператор интегрирования.