Системы с пассивной адаптацией

Адаптивные системы применяются, если диапазон изменения свойств ОУ и внешних воздействий настолько велик, что показатель качества выходит за пределы заданных ограничений.

С другой стороны любая неадаптивная система с отрицательной обратной связью (ОС) в силу заложенного в неё принципа управления по отклонению способна нейтрализовать изменение внешних воздействий и характеристик ОУ, но в небольшом диапазоне. Если расширить этот диапазон, то можно нейтрализовать значительные изменения внешних воздействий и характеристик ОУ, т.е. можно получить неадаптивную систему, обладающую свойствами адаптивных систем без специального использования принципов адаптации.

Расширение подобных функциональных возможностей неадаптивных систем можно выполнить за счёт:

- больших коэффициентов усиления разомкнутых систем;

- автоколебательных режимов;

- систем с переменной структурой.

Такие системы называются системами с пассивной адаптацией.

В качестве примера рассмотрим замкнутую систему с большим коэффициентом усиления в разомкнутом состоянии.

Пусть замкнутая система состоит из УУ с передаточной функцией

и ОУ с передаточной функцией

. Введём дополнительную отрицательную обратную связь с коэффициентом передачи

(рис. 10.6).

Рисунок 10.6 – Схема автоматизации с двумя отрицательными обратными связями

Определяем передаточную функцию всей системы :

; .

Тогда ;;

В результате получаем выражение для передаточной функции системы:

. (10.20)

Чтобы устранить влияние передаточной функции объекта управления на передаточную функцию выберем передаточную функцию УУ с очень большим коэффициентом передачи:

, (10.21)

где 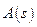и 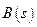- полиномы;

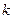- коэффициент передачи .

Тогда передаточную функцию (10.20) можно привести к виду:

. (10.22)

Отсюда следует, что передаточная функция замкнутой системы не зависит от свойств ОУ и определяется только свойствами устройств дополнительной отрицательной обратной связи .

Однако неограниченное увеличение коэффициента усиления разомкнутой системы приводит к неустойчивости замкнутой системы. Чтобы система была устойчивой необходимо, чтобы сумма порядков (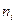) полинома в знаменателе (10.21) (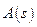) не превышала сумму порядков () полинома в числителе (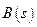) на два, т.е. чтобы выполнялось условие

; . (10.23)

Таким образом, стабилизировать передаточную функцию замкнутой системы можно за счёт неограниченного увеличения коэффициента усиления 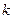лишь при соблюдении условия устойчивости системы (10.23).