Аналитическое конструирование регуляторов методом динамического программирования
Рассмотрим решение задач АКР методом динамического программирования на примере задачи о регуляторе состояния.
Пусть линейный нестационарный объект описывается уравнением состояния (8.1)
 .
.
В качестве критерия качества используем (8.5):
 .
.
По стандартной методике (см. п.5.3) записываем уравнение Беллмана (5.21):
 .
.
Обозначим через  минимальное значение критерия качества
минимальное значение критерия качества  :
:

 , (8.27)
, (8.27)
где  - подынтегральная функция.
- подынтегральная функция.
С учётом этого уравнение Беллмана примет вид:
 . (8.28)
. (8.28)
Дальнейшая техника поиска оптимального управления для уравнения Беллмана в форме (8.28) полностью совпадает с методикой (см. п.5.3) для уравнения Беллмана (5.21).
1. Так как на управление  ограничений не наложено, оптимальное управление ищем из условия равенства нулю частной производной по
ограничений не наложено, оптимальное управление ищем из условия равенства нулю частной производной по  от выражения в фигурных скобках уравнения (8.28):
от выражения в фигурных скобках уравнения (8.28):
 .
.
Откуда определяем, что
 . (8.29)
. (8.29)
2. Чтобы найти функцию  , подставим
, подставим  (8.29) в выражение в фигурных скобках уравнения Беллмана (8.28) и получим уравнение типа Гамильтона-Якоби, независящее от управления
(8.29) в выражение в фигурных скобках уравнения Беллмана (8.28) и получим уравнение типа Гамильтона-Якоби, независящее от управления  :
:


 .
.
В итоге, уравнение Гамильтона-Якоби примет вид:
 . (8.30)
. (8.30)
3. Выберем граничные условия. Из (8.27) видно, что при 
 . (8.31)
. (8.31)
При  введём пока неизвестную симметричную нестационарную
введём пока неизвестную симметричную нестационарную  матрицу
матрицу  , при которой выполняется равенство:
, при которой выполняется равенство:
 , (8.32)
, (8.32)
причём  .
.
Так как  , а
, а  , то, подставив (8.32) в уравнение Гамильтона-Якоби (8.30), получим:
, то, подставив (8.32) в уравнение Гамильтона-Якоби (8.30), получим:
 . (8.33)
. (8.33)
В дальнейшем для простоты не будем записывать зависимость от времени  .
.
Так как  , то уравнение (8.33) запишем в форме:
, то уравнение (8.33) запишем в форме:
 .
.
Это условие выполняется при любых состояниях  , если выражение в скобках равно нулю, т.е. если
, если выражение в скобках равно нулю, т.е. если
 .
.
Откуда следует, что
 . (8.34)
. (8.34)
В результате получили нелинейное квадратичное относительно матрицы  дифференциальное уравнение, называемое матричным уравнением Риккати.
дифференциальное уравнение, называемое матричным уравнением Риккати.
Уравнение Риккати в основном решается с помощью ЭВМ, начиная с  и полагая, что
и полагая, что  . Для этого приближённо принимают, что
. Для этого приближённо принимают, что
 ,
,
где 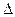 - малое приращение времени.
- малое приращение времени.
Это позволяет представить уравнение Риккати (8.34) в следующей форме:
 .
.
4. Найдя матрицу  , можно по формуле (8.32) определить
, можно по формуле (8.32) определить  и, подставив его в выражение (8.29), найти оптимальное управление
и, подставив его в выражение (8.29), найти оптимальное управление  .
.
В работах Калмана доказано, что для стационарных объектов можно ввести матрицу  , где
, где  - постоянная симметричная положительно определённая матрица. Эта матрица определяется из уравнения Риккати, в котором следует положить
- постоянная симметричная положительно определённая матрица. Эта матрица определяется из уравнения Риккати, в котором следует положить  . Тогда нелинейное матричное уравнение Риккати примет вид:
. Тогда нелинейное матричное уравнение Риккати примет вид:
 . (8.35)
. (8.35)