Динамическое программирование в задаче о максимальном быстродействии

Задачу о максимальном быстродействии можно представить как задачу с закреплённым правым концом траектории (задано), нефиксированным временем и критерием оптимальности

. (7.3)

При сравнении критериев (6.2) и (7.3) видно, что для максимального быстродействия . Если в уравнении Беллмана (5.21) положить, что , , а заменить на , то получится уравнение Беллмана в задаче о максимальном быстродействии:

(7.4)

или в скалярной форме

, (7.5)

где - непрерывная функция, которая имеет непрерывные частные производные по переменной .

Рассмотрим методику определения оптимального управления методом динамического программирования в задаче о максимальном быстродействии. Как и в случае динамического программирования (см. п.5.3), из условия минимума выражения в фигурных скобках находится оптимальное управление . Потом, подставив полученное оптимальное управление в уравнение Беллмана (7.5), получаем дифференциальное уравнение первого порядка в частных производных типа Гамильтона-Якоби для задачи о максимальном быстродействии (см. методику определения оптимального управления с помощью уравнения Беллмана, п.5.3). С учётом граничного условия находим и, подставив его в выражение для оптимального управления , получаем искомое оптимальное управление .

Наиболее часто для решения таких задач используются численные методы, реализуемые с помощью ЭВМ.

Для простоты рассмотрим задачу о максимальном быстродействии для линейного объекта, описываемого уравнением состояния:

, (7.6)

или в векторной форме

, (7.7)

где - матрица с элементами , ;

- матрица с элементами , , .

Область допустимых управлений наиболее часто задаётся системой неравенств

, (7.8)

где .

С учётом того, что , то уравнение Беллмана (7.4) для линейного объекта примет вид:

.

Так как первое слагаемое не зависит от 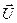, то его можно вынести за знак операции минимизации, что приведёт к уравнению

(7.9)

или в скалярной форме

. (7.10)

Чтобы слагаемое в фигурных скобках было минимальным необходимо, чтобы оно было отрицательным и принимало наибольшее значение по модулю. Это условие выполняется, если в (7.8) положить, что . Чтобы при отрицательном множителе выражение в фигурных скобках (7.10) было отрицательным необходимо, чтобы было положительным или наоборот. Учитывая это, можно записать, что

, , (7.11)

где при при *.

Из (7.11) следует, что оптимальные управления в задаче о максимальном быстродействии являются кусочно-постоянными функциями, принимающими дискретные значения: либо , либо в зависимости от множителя (рис. 7.2).

 

Рисунок 7.2 – График изменения оптимального управления в задаче о максимальном быстродействии

 

* Свойства функции сигнум приведены в приложении А

 

Учитывая, что и, подставив оптимальное управление (7.11) в уравнение Беллмана (7.10), получим:

;

. (7.12)

Решив уравнение (7.12), можно найти и, подставив его в (7.11), определяем оптимальное управление , .