Связь между моментами силы относительно полюса и оси

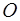Теорема. Проекция момента силы относительно полюса на ось , проходящую через этот полюс, равна моменту силы относительно оси :

.

Доказательство:

Для доказательства вычислим левую и правую части предполагаемого равенства и убедимся, что результаты вычислений совпадают (рис. 22).

 

 

 

 

Момент силы относительно полюса 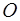перпендикулярен плоскости треугольника и по величине . Обозначим угол между и осью через . Тогда проекция на ось :

Проведем через полюс 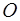плоскость, перпендикулярную оси и вічислим момент силі относительно оси :

(рассматривается случай, когда стремится повернуть плоскость вокруг оси против хода часовой стрелки).

Воспользуемся простым положением элементарной геометрии: площадь проекции плоской фигуры () на некоторую плоскость () равна площади проектируемой фигуры (), умноженной на косинус угла между плоскостью проекции и плоскостью проектируемой фигуры. Угол между двумя плоскостями – это угол между перпендикулярами к этим плоскостям в их общей точке, то есть угол . Тогда . Следовательно

.