Свойства математического ожидания.
1. Математическое ожидание постоянной равно этой постоянной
M[C]=C, т.к. С можно рассматривать как дискретную величину.
2. Постоянный множитель выносится за знак математического ожидания M[Cх]=C M[х]
Доказательство: Для дискретных величин, постоянную выносим за знак суммы, для непрерывных можно выносить за знак интеграла.
3. Математическое ожидание 2-х случайных величин равно сумме их математических ожиданий.
M[x+y]=M[x]+M[y]
4. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий
M[x×y]=M[x]×M[y]
Можно обобщить на произвольное число сомножителей при условии их независимости.
Пример: Найти математическое ожидание суммы числа очков, которые могут выпасть при бросании двух игральных кубиков.
x – число очков на первом кубике;
y - число очков на втором кубике;
| x | ||||||
| Р | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Найти математическое ожидание для x и для y.
M[x]=1×1/6+2×1/6+3×1/6+4×1/6+5×1/6+6×1/6=1/6+2/6+3/6+4/6+5/6+6/6=21/6= 3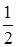 =7/2;
=7/2;
M[y]=7/2+7/2=14/2=7.
Итак, мы познакомились с одной из основных числовых характеристик случайной величины- математическим ожиданием , которое характеризует среднее значение случайной величины, около него группируются все возможные значения случайной величины.