Прямая и точка в плоскости.

Точка принадлежит плоскости, если она принадлежит какой-нибудь прямой, лежащей в этой плоскости.

Из элементарной геометрии известно, что прямая принадлежит плоскости, если:

o oна проходит через две точки, принадлежащие плоскости;

o oна проходит через 1 точку, принадлежащую плоскости, и параллельна прямой, лежащей в плоскости.

Из первого положения следует, что если прямая принадлежит плоскости, то ее одноименные следы лежат на одноименных следах плоскости.

Рис.1

 

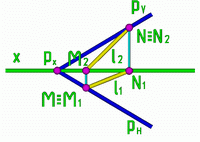Рис.2

Пусть следами задана плоскость общего положения Р, построим в этой плоскости прямую l.