Программирование ветвлений
| |
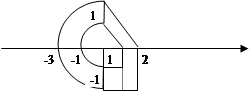
 Задача №1. Определить, попадет ли точка с координатами (х, у ) в заштрихованную область.
Задача №1. Определить, попадет ли точка с координатами (х, у ) в заштрихованную область.
 | |||
|
Исходные данные: х,у
Результат: да или нет
Математическая модель:
Ok=I || II || III || VI, где I, II, III, IV – условия попадания точки в заштрихованную область для каждого квадранта.
Квадрант I: Область формируется прямыми 0Х и 0У, прямой, проходящей через точки (0,1)и(1,0) и прямой, проходящей через точки (0,3) и (2,0).
Необходимо определить уравнения прямых у=ax+b. Решаем две системы уравнений:
1) 1=a*0+b;
0=a*1+b;
2) 2=a*0+b;
0=a*3+b;
Из этих систем получаем следующие уравнения прямых:
y=-1x+1;
y=-2/3x+1;
Тогда условие попадания точки в I квадрант будет выглядеть следующим образом:
y>=-x+1&&y<=-2/3x+2&&y>=0&&x>=0.
Квадранты II и III: Область формируется прямыми 0Х и 0У и двумя окружностями, описываемыми формулами x2+y2=1, x2+y2=9.
Тогда условие попадания точки во II и III квадранты будет выглядеть следующим образом:
x2+y2>=1&& x2+y2<=9&&&&x<=0.
Квадрант IV:
Область формируется двумя прямоугольниками. Точка может попадать либо в первый прямоугольник, либо во второй.
Условие попадания точки в IV квадрант будет выглядеть следующим образом:
(x>=0&&x<=1&&y<=-1&&y>=-3)|| (x>=1&&x<=3&&y<=0&&y>=-3) .
Программа:
#include <iostream.h>
#include <math.h>
void main()
{
float x,y;
cout<<"\nEnter x,y";
cin>>x>>y;
bool Ok=(y>=-x+1&&y<=2/3*x+2&&x>=0&&y>=0)||
(pow(x,2)+pow(y,2)>=1&&pow(x,2)+pow(y,2)<=9&&x<=0)||
(x>=0&&x<=1&&y<=-1&&y>=-3)||(x>=1&&x<=2&&y<=0&&y>=-3);
cout<<"\n"<<Ok;
}
Тесты:
| Квадрант | Исходные данные (X,Y) | Результат (Ok) |
| I | 0.2,0.2 | |
| I | 0.7,0.5 | |
| II | -0.5, 0.5 | |
| II | -2,0 | |
| III | -0.5,-0,5 | |
| III | -2,-1 | |
| IV | 0,5,-0.5 | |
| IV | 1.5, -1 | |
| Центр системы координат | 0,0 |