Импеданс излучения.

Анализируемая модель представлена на рис. 3. Пьезоэлемент состоит из пьезослоя 2 и металлических обкладок 1 (наслоя) и 3 (подслоя). Последний находится в акустическом контакте со звукопроводом 4. Рассмотрим в соответствии с работой [7] наиболее важные в практическом отношении случаи преобразователей на основе пьезоэлектрика класса 6mm (например CdS, ZnO) с осью 6 , перпендикулярной или параллельной поверхностям электродов. В первом случае возбуждаются чисто продольные упругие волны, а во втором- сдвиговые. Надслой, подслой и звукопровод будем считать изотропными или ориентированными продольной нормалью перпендикулярно торцу последнего. В противном случае преобразователь будет одновременно возбуждать квазипродольные и квазипоперечные волны. (Случай произвольной ориентации пьезоэлектрика рассмотрен в работе [8].) Полагая d/dx=d/dy=0, для непроводящего пьезоэлектрика из уравнения Пуассона получим dD/dz=0, где D- электрическое смещение. Это означает, что величина Dне зависит от координаты z и может быть функцией только времени t. При выбранной ориентации уравнения состояния пьезоэлектрика сводятся к скалярным

где Tи u- упругое напряжение и механическое смещение в пьезоэлектрике, Cи e- упругая и пьезоконстанты, ε- диэлектрическая проницаемость, E - напряженность электрического поля. Если ось 6 пьезоэлектрика перпендикулярна (параллельна) торцу звукопровода, то физические константы в уравнениях (53) и (54), как показано в разделе 2.4, представляют собой следующие компоненты тензоров: e=e₃₃₃ (=e₁₁₃) , ε=ε₃₃ (=ε₁₁) , C=C₃₃₃₃ (=C₁₃₁₃). Импеданс пьезоэлемента в квазистатическом приближении определяется следующим образом:

где s - площадь подслоя. Если найти E из (54) и подставить в (55), то получим

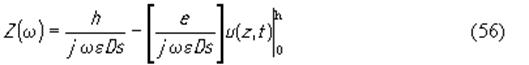
Первый член в этом выражении представляет собой чисто реактивное сопротивление, определяемое статической емкостью C₀ =εs/h . Действительная часть второго члена является сопротивлением излучения R(ω) , а мнимая - входит в реактивное сопротивление преобразователя как некоторая добавка, вызванная пьезоэффектом. Функция u(z,t) есть решение волнового уравнения (18) для пьезоэлектрика:

где u₀₊ и u_0- - комплексные амплитуды, определяемые граничными условиями, β=ω(ρ/(C(K² +1)))^1/2 , ρ- плотность, K - коэффициент электромеханической связи. В случае нормальной ориентации пьезоэлектрика

а в случае тангенциальной -

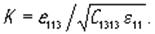
Если исходить из непрерывности на границах двух сред механических смещений и упругих напряжений, то при z=0 и z=h должны быть равны акустические импедансы, определяемые формулой (38), найденные в пьезоэлектрике и в контактирующей с ним среде. Тогда для звукопровода, имеющего бесконечную длину, получим следующие граничные условия:

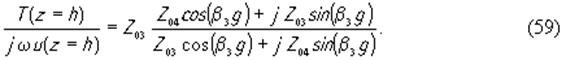
Формула (58) означает, что пьезоэлемент нагружен надслоем, как короткозамкнутым отрезком волновода, а последнее равенство выражает тот факт, что подслой является трансформатором сопротивления, включенным между бесконечно длинным звукопроводом с волновым сопротивлением Z₀₄и пьезоэлементом (см. формулу (44). Здесь Z₀₁, Z₀₃, Z₀₄- акустические волновые сопротивления соответственно надслоя, подслоя и звукопровода , β₁ и β₃- волновые числа в первой и третьей среде (см рис. 3). Для того, чтобы выразить в (58) и (59) величину T при z=0и z=h через смещения u, воспользуемся следующим из (53) и (54)соотношением

Подставляя его совместно с (57) в (58) и (59), нетрудно получить два линейных алгебраических уравнениях, в которых неизвестными будут u₀₊ u_0- . Решение этих уравнений и подстановка результатов в (57) и (56) приводят к аналитическому выражению для безразмерного активного сопротивления излучения

где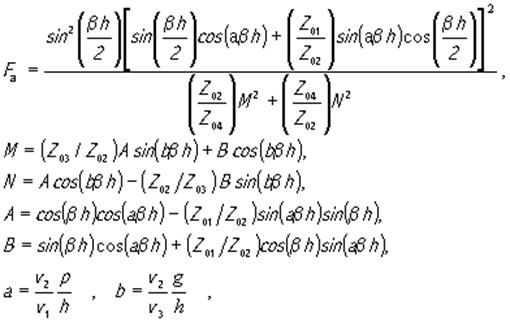
где v₁ , v₂ , v₃ - скорости звука соответственно в надслое, пьезоэлектрике и подслое. Частота не входит в полученную формулу в явном виде и представлена в ней только безразмерной величиной βh . В этом смысле формула (61) имеет универсальный характер, а вычисленное по ней значение δможет быть отнесено к любой частоте.
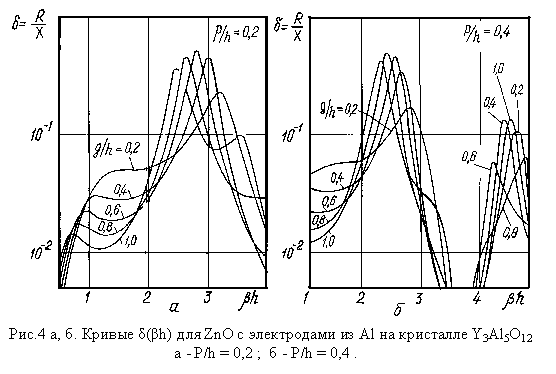
Из выражения (56) находится также реактивная составляющая импеданса излучения. Формула для нее оказывается более громоздкой, чем (61), и здесь не приводится в связи с тем, что при использовании известных пьезоэлектриков и материалов подслоя и надслоя, реактивность преобразователя с достаточной для практики точностью определяется емкостным сопротивлением 1/ωC₀ . Максимальное значение добавки, обусловленной пьезоэффектом, обычно не превышает 0,3/ωC₀ , да и то это имеет место при значениях, соответствующих малым величинам R(ω). На рис. 4 а,б при p/h=0,2 и 0,4 соответственно показана зависимость δ(βh), вычисленная по формуле (61), для преобразователя из ZnO с надслоем и подслоем из Al на кристалле Y₃Al₅O₁₂ . Плоскость преобразователя перпендикулярна направлению [0001] в пьезоэлектрике и [111] в звукопроводе. Кривые 1-5 соответствуют g/h= 0,2; 0,4; 0,6; 0,8; 1,0. При вычислениях использовали физические константы для ZnO, Y₃Al₅O₁₂ и Al соответственно: скорость звука ( 10³ м/с) 6,1; 8,6; 6,32; акустические волновые сопротивления (10⁶ кг/м с) 34,4; 39,2; 17,1; диэлектрическую проницаемость и коэффициент электромеханической связи ZnO: 8,84 и 0,283. Из рис.4 следует, что изменение g/h слабо влияет на ход кривых, тогда как вариации p/h существенно изменяют их ход. Эти обстоятельства обуславливают более жесткие технологические требования к изготовлению надслоя, чем подслоя. Приведенные кривые для заданной частоты ωпозволяют выбрать значение βh, соответствующее подходящей величине δ(например, максимуму на одной из кривых δ(βh)) и вычислить требуемую толщину h=(β₀h)v₂/v₁ , а затем и толщины pи g. Задавая площадь s, нетрудно вычислить емкостное сопротивление преобразователя:

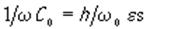
и найти сопротивление излучения

 

Каждому значению βhна оси абсцисс можно привести в соответствие частоту f=(βh)v₂/2πh и, таким образом, для конкретного преобразователя при выбранной толщинеhполучить в явном виде зависимостьR(f).