Нелинейные модели парной регрессии и корреляции

Различают два класса нелинейных регрессий:

1. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например

· полиномы различных степеней – , ;

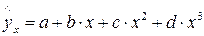· равносторонняя гипербола – ;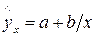

· полулогарифмическая функция – .

2. Регрессии, нелинейные по оцениваемым параметрам, например

· степенная – ;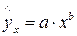

· показательная – ;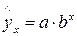

· экспоненциальная – .

Регрессии нелинейные по включенным переменным приводятся к линейному виду простой заменой переменных (линеаризация), а дальнейшая оценка параметров производится с помощью метода наименьших квадратов. Рассмотрим некоторые функции.

Парабола второй степени приводится к линейному виду с помощью замены: . В результате приходим к двухфакторному уравнению , оценка параметров которого при помощи МНК, приводит к системе следующих нормальных уравнений:

А после обратной замены переменных получим

(1.17)

Парабола второй степени обычно применяется в случаях, когда для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую.

Равносторонняя гипербола 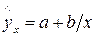приводится к линейному уравнению простой заменой: . Система линейных уравнений при применении МНК будет выглядеть следующим образом:

(1.18)

Аналогичным образом приводятся к линейному виду зависимости , и другие.

Несколько иначе обстоит дело с регрессиями нелинейными по оцениваемым параметрам, которые делятся на два типа: нелинейные модели внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием) и нелинейные модели внутренне нелинейные (к линейному виду не приводятся).

К внутренне линейным моделям относятся, например, степенная функция – 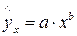, показательная – 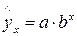, экспоненциальная – , логистическая – , обратная – .

К внутренне нелинейным моделям можно, например, отнести следующие модели: , .

Среди нелинейных моделей наиболее часто используется степенная функция , которая приводится к линейному виду логарифмированием:

,

где . Т.е. МНК мы применяем для преобразованных данных:

а затем потенцированием находим искомое уравнение.

Широкое использование степенной функции связано с тем, что параметр в ней имеет четкое экономическое истолкование – он является коэффициентом эластичности.

Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%. Формула для расчета коэффициента эластичности имеет вид:

. (1.19)

Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора 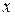, то обычно рассчитывается средний коэффициент эластичности:

. (1.20)

Приведем формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии: