Электрофорез и электроосмос
Существование рассмотренных выше явлений электрофореза и электроосмоса объясняется наличием ДЭС у межфазной границы.
На рис. 7.5 приведена схема ДЭС по Гельмгольцу.
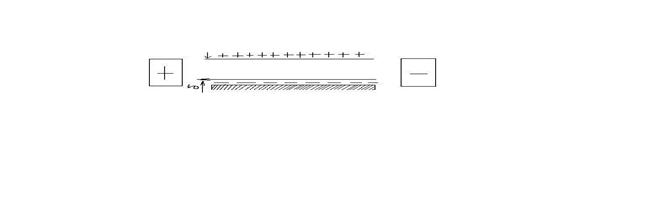
Рис. 7.5. Поведение ДЭС при электрокинетических явлениях
При наложении электрического поля противоионы жидкости стремятся сдвинуться к катоду. Вместе с ними стремится передвинуться вся жидкость, в то время как твердая поверхность должна двигаться в противоположном направлении. В зависимости от того, какая фаза неподвижна, наблюдается электрофорез или электроосмос.
Если смещать одну фазу относительно другой, то происходит перенос зарядов и возникает электрический ток и разность потенциалов. В зависимости от того, передвигается жидкость относительно неподвижной стенки или твердые частицы в жидкости, наблюдается потенциал течения или потенциал седиментации.
Пусть d – расстояние между потенциалопределяющими ионами и противоионами, а s – поверхностная плотность электричества, которая равна заряду жидкости с противоположным знаком. Эту систему можно рассматривать как конденсатор с разностью потенциалов между его обкладками z. Для плоскопараллельного конденсатора известна зависимость
z = 4pds/e , (7.3)
где e – диэлектрическая проницаемость. Это уравнение можно записать иначе:
s=ez/4pd. (7.4)
Если тангенциально к ДЭС приложить разность потенциалов Е, а расстояние между электродами L, то градиент потенциала внешнего поля Н определится как
H = E/ L. (7.5)
Электрическая сила, действующая тангенциально на единицу межфазной поверхности, находящейся в электрическом поле с градиентом потенциала Н, и стрямящаяся сдвинуть фазы относительно друг друга, равна
F1 = s H.
Сила трения на единицу поверхности раздела фаз по закону Ньютона определяется по формуле
F2 = h (du/dl),
где h – динамическая вязкость жидкости, u – скорость движения жидкости относительно твердой стенки, l – толщина слоя жидкости, в котором меняется ее скорость (при данной схеме ДЭС l = d).
Приняв, что скорость течения жидкости в ДЭС линейно меняется с расстоянием, получим
F2 = h (u/ d). (7.6)
В стационарных условиях F1 = F2 или
H = (u/ d). (7.7)
Подставив s из (7.4), получим уравнение Гельмгольца – Смолуховского:
U = ezH/ (4 ph). (7.8)
Скорость электрофоретического переноса можно отнести к единице градиента приложенного потенциала и получить
u0 = u/ H = ez / ( 4 ph ). (7.9)
Здесь u0 – электрофоретическая подвижность. Решив уравнение (7.8) относительно дзета-потенциала, получим
z=4phu / (eH ). (7.10)
По этой формуле расчет дзета-потенциала проводят при электрофорезе и электроосмосе, если известно значение u.
Если Е измеряется в вольтах, L– в сантиметрах, то H = E/L = E/L .300 (эл.-ст.ед./см ). Откуда потенциал в абсолютных электростатических единицах находится по уравнению
z=4phu /(eH)=4phuL 300/ (eE ). (7.11)
Обычно дзета-потенциал выражают в вольтах, в этом случае значение, найденное по (7.11), следует умножить на 300, т. е.
z=4phuL.3002/(eE) . (7.12 )
При выводе сделан ряд упрощений. ДЭС представляет из себя не плоскопараллельный конденсатор, а конденсатор, одна из обкладок которого состоит из диффузно распределенных ионов. Допущение, что du/dl = u/l, условно, так как скольжение идет не в плоскости, а в слое конечной толщины, содержащем некоторое число противоионов. Изменение скорости в этом слое от расстояния не строго прямолинейно. Вязкость и диэлектрическая проницаемость в ДЭС и в объеме раствора могут быть отличными друг от друга, что также не учитывалось.