ПОСТРОЕНИЕ ПЛОСКИХ ФИГУР

 

Построение многоугольника, равного данному, можно выполнить так, что его стороны будут располагаться парал­лельно соответствующим сторонам заданного многоугольника, или построенный многоуголь­ник будет повернут в плоскости относительно заданного. И в том, и в другом случае решение

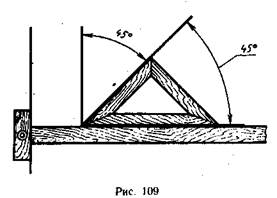
Деление. прямого угла пополам с помощью угольника с углами 45, 45 и 90° и рейсшины показано на рис. 109.

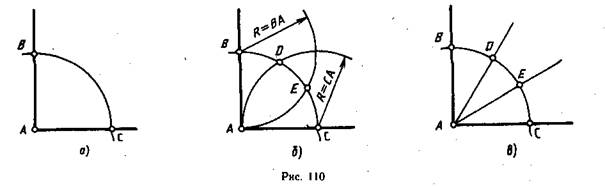
Деление прямого угла на три равные части выполняется циркулем или с помощью угольника и рейсшины. При делении угла циркулем из вершины А произвольным радиусом проводят дугу до пересечения со сто­ронами угла в точках В и С (рис. ПО, а). Затем тем же радиусом из точек В и С делают на дуге засечки, получают точки D и Е (рис. 110, б), которые соединяют с точкой А. Прямые АЕ и AD делят прямой угол на три равные части (рис. 110, в).

Деление прямого угла на три равные части с помощью рейсшины и угольника с углами 30, 60 и 90° показано на рис. 111.

задачи сводится к построению третьей точки относительно двух заданных.

Например, на плоскости заданы точки А и В (рис. 112, а). Требуется построить точку С, расположенную выше заданных точек на рас­стоянии п от точки Л, и т от точки В. Мно­жество точек, которые находятся на расстоянии п от точки Л, располагается на окружности с центром в точке А радиусом R=n. Множе­ство точек, которые располагаются на расстоя­нии т от точки В, находился на окружности с центром в точке В радиусом R₁=m (рис. 112,6). В пересечении этих окружностей полу­чают точки С и C₁. Из двух полученных точек выбирают нужную. Проводить окружности пол­ностью не обязательно, достаточно провести две короткие дуги (рис. 112, в).

На рис. 113, а задан многоугольник ABCDE. Требуется построить равный ему многоуголь­ник A₁B₁C₁D₁E₁. Построение многоугольника A₁B₁C₁D₁E₁можно начать с построения любой его стороны, например стороны А₁В₁. Для это­го параллельно стороне АВ проводят прямую и на ней циркулем откладывают отрезок A₁B₁ равный отрезку АВ. Затем циркулем измеряют расстояние от, точки А до точки С и этим радиусом из точки А₁ проводят дугу в направ­лении строящейся точки С₁ также от точки В измеряют расстояние до точки С и этим радиусом из точки В₁ проводят дугу до пере­сечения с первой дугой в точке С₁. Соединив точку С₁ с точкой В₁ прямой линией, полу­чают вторую сторону многоугольника В₁С₁ (рис. 113, б). Для построения точки D₁ изме­ряют расстояние от точки D до двух других вершин многоугольника (например А и В, или В и С, или С и А).

 

 

 

 

 

На рис. 113, 0 взяты расстоя­ния от точек В и С. Дугу из точки В₁ проводят радиусом, равным отрезку BD, а из точки d радиусом, равным отрезку CD. Пересечение этих дуг дает точку D₁. Соединив точку D₁ с точкой C₁, получают сторону многоугольника C₁D₁ (рис. 113, в). Аналогично строят точку Е₁

(рис. 113,г).