Числовые характеристики случайных величин
Во многих практических случаях не требуется знания полного закона распределения СВ. Зачастую бывает достаточно указать (определить) некоторые числовые параметры, в определенной степени характеризующие распределение. Такие параметры называют числовыми характеристиками СВ. Обычно их подразделяют на характеристики положения (математическое ожидание, мода, медиана, начальные моменты различных порядков) и характеристики рассеивания (дисперсия, среднее квадратическое отклонение, центральные моменты различных порядков). Числовые характеристики в сжатой форме определяют наиболее существенные черты распределения СВ. Важнейшими из них для эконометрического анализа являются математическое ожидание, дисперсия, среднее квадратическое отклонение.
Математическое ожидание М(х) характеризует среднее ожидаемое значение СВ Х. Например, при оценивании покупательской способности населения необходимо знание среднего дохода. При анализе выгодности двух видов деятельности на начальном этапе можно ограничиться сравнением их средних прибыльностей.
Математическое ожидание М(х) определяется следующим образом:
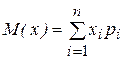. (1.4)
для дискретной СВ с n ее возможными значениями;
. (1.5)
для непрерывной СВ.
Рассчитаем М(х) для дискретной СВ Х (пример 1.1):
М(х) = 3 · 0,5 + 4 · 0,3 + 5 · 0,2 = 3,7.
Свойства математического ожидания
1. М(С) = С, где С - константа.
2. М(СХ) = С· М(Х).
3. M(X ± Y) = M(X) ± M(Y).
4. M(aX + b) = a · M(X) + b, где а и b - константы.
5. Для независимых СВ Х и Y M(XY) = M(X) · M(Y).
Для детального анализа поведения СВ знания лишь близкого к среднему значению математического ожидания явно недостаточно, так как при сравнении случайных величин, имеющих одинаковые математические ожидания, часто обнаруживаются их существенные различия. Например, средний уровень жизни в Швеции и США приблизительно одинаков, однако разброс в доходах населения в этих странах существенно отличается. Акции двух компаний могут приносить в среднем одинаковые дивиденды, однако вложение денег в одну из них может быть гораздо более рискованной операцией, чем в другую [11]. Следовательно, необходима числовая характеристика, которая оценивает разброс (отклонение, рассеяние, вариацию) значений СВ относительно ее математического ожидания. Такой характеристикой является дисперсия D(Х).
Дисперсией СВ Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
D(x) = M(x - M(x))2 = M(x2) – M2(x). (1.6)
Дисперсия для дискретной СВ рассчитывается по формуле:
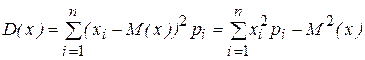. (1.7)
Для непрерывной СВ:
. (1.8)
Дисперсия СВ Х из примера (1.1) равна:
D(x) = (3 - 3,7)2 · 0,5 + (4 - 3,7)2 · 0,3 + (5 - 3,7)2 · 0,2 = 0,61.
Свойства дисперсии:
1. D(C) = 0, где С – константа;
2. D(CX) = C2D(X);
3. D(X ± Y) = D(X) + D(Y), где Х и Y – независимые СВ;
4. D(aX + b) = a2D(X), где а и b – константы.
Дисперсия имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому, чтобы представить разброс значений в тех же единицах, что и сама СВ, используется числовая характеристика, называемая средним квадратическим отклонением (стандартным отклонением) и равная арифметическому значению квадратного корня из дисперсии СВ Х:
. (1.9)
Чтобы оценить разброс значений СВ в процентах относительно ее среднего значения, вводится числовая характеристика, которая называется коэффициентом вариации V(X), и рассчитывается по формуле:
. (1.10)
Дисперсия, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии распределения (отношение центрального момента третьего порядка μ3 к кубу среднего квадратического отклонения – μ3/σ3(Х)), кроме оценивания рассеивания значений СВ, служат для оценки риска различных действий со случайным исходом, выступая в качестве показателей уровня риска различных направлений функционирования экономических систем в условиях неопределенности. Например, эти характеристики могут быть использованы при анализе риска инвестирования в ту или иную отрасль, при оценивании различных активов в портфеле и портфеля активов в целом и т. д. [6,34].