Ход решения задачи
Метод наложения (метод суперпозиции) применяется для расчета сложных электрических цепей постоянного тока несколькими источниками энергии. Наиболее целесообразно применять его при небольшом числе источников. По сравнению с другими методами он имеет преимущества в тех случаях, когда не требуется полный расчет цепи, а можно ограничиться, например, только определением токов на участках электрической цепи с источником питания.
Таблица 4.1
Исходные данные к задаче № 4
| Вариант | Величины | Схема | ||||||||||
 , В , В
| 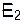 , В , В
|  , Ом , Ом
|  , Ом , Ом
| 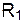 , Ом , Ом
|  , Ом , Ом
|  , Ом , Ом
|  , Ом , Ом
|  , Ом , Ом
|  , Ом , Ом
| 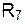 , Ом , Ом
| ||
| 0,1 | 0,05 | Рис. 4.1, а | ||||||||||
| 0,1 | 0,05 | Рис. 4.1, а | ||||||||||
| 0,1 | 0,05 | Рис. 4.1, а | ||||||||||
| 0,1 | 0,05 | Рис. 4.1, а | ||||||||||
| 0,1 | 0,05 | Рис. 4.1, а | ||||||||||
| 0,1 | 0,05 | Рис. 4.1, б | ||||||||||
| 0,1 | 0,05 | Рис. 4.1, б | ||||||||||
| 0,1 | 0,05 | 2,5 | Рис. 4.1, б | |||||||||
| 0,1 | 0,05 | Рис. 4.1, б | ||||||||||
| 0,1 | 0,05 | Рис. 4.1, в | ||||||||||
| 0,15 | 0,1 | Рис. 4.1, в | ||||||||||
| 0,15 | 0,1 | Рис. 4.1, в | ||||||||||
| 0,15 | 0,1 | Рис. 4.1, в | ||||||||||
| 0,15 | 0,1 | Рис. 4.1, г | ||||||||||
| 0,15 | 0,1 | Рис. 4.1, г | ||||||||||
| 0,2 | 0,15 | Рис. 4.1, г | ||||||||||
| 0,2 | 0,15 | Рис. 4.1, г | ||||||||||
| 0,2 | 0,15 | Рис. 4.1, д | ||||||||||
| 0,2 | 0,15 | Рис. 4.1, д | ||||||||||
| 0,2 | 0,15 | Рис. 4.1, д | ||||||||||
| 0,1 | 0,05 | Рис. 4.1, д | ||||||||||
| 0,1 | 0,05 | Рис. 4.1, е | ||||||||||
| 0,1 | 0,05 | Рис. 4.1, е | ||||||||||
| 0,1 | 0,05 | 0,5 | 0,5 | 0,5 | Рис. 4.1, е | |||||||
| 0,1 | 0,05 | Рис. 4.1, е |
Метод наложения заключается в том, что воздействие нескольких источников питания (ЭДС и напряжений) на электрическую цепь можно рассматривать как результат воздействия на нее каждого из источников независимо от воздействия других источников, имеющихся в данной электрической цепи. При этом в каждой из ветвей электрической цепи ток определяется как алгебраическая сумма токов, вызываемых в ней действием каждого из источников. В процессе расчета по методу наложения рассматриваемая электрическая цепь с несколькими источниками ЭДС и напряжений заменяется расчетными электрическими цепями с одним источником, число которых равно числу источников, действующих в электрической цепи. Другие источники питания, кроме рассматриваемого, при этом закорачиваются, т.е. удаляются из цепи.
В результате расчета каждой из этих преобразованных цепей определяются частичные токи от действия данного источника. Значение действительных токов ветвей определяется алгебраическим суммированием частичных токов в этих ветвях.
Применительно к исходной электрической цепи (рис. 4.2, а), на которой предварительно нанесены положительные направления токов в ветвях, на рис. 4.2, б, в приведены расчетные электрические цепи для частичных токов от действия ЭДС  и
и 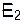 .
.
а

| б

| в

|
| Рис. 4.2. Сложная электрическая цепь постоянного тока (а) и совокупность двух схем для ее расчета методом наложения: б – от действия ЭДС Е1; в – от действия ЭДС Е2 |
При расчете этих цепей определяются частичные токи во всех ветвях. С учетом направления частичных токов и токов в ветвях исходной электрической цепи определяют действительные токи в ветвях рассматриваемой цепи путем наложения (алгебраического суммирования) частичных токов в ветвях:  ;
;  ;
;  .
.
Правильность расчёта необходимо проверить по балансу мощностей. Суммарная мощность источников электрической энергии  равна общей мощности, поглощаемой сопротивлениями нагрузки (потребителями)
равна общей мощности, поглощаемой сопротивлениями нагрузки (потребителями)  , входящими в состав цепи, т.е.
, входящими в состав цепи, т.е.

Относительная ошибка  должна быть меньше наперёд заданного числа, например, 5 %:
должна быть меньше наперёд заданного числа, например, 5 %:  .
.