ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ МАТЕМАТИЧЕСКИХ ОЖИДАНИЙ ПРОВЕРКА ГИПОТЕЗЫ О РАВЕНСТВЕ ВЕРОЯТНОСТЕЙ, ДРУГИЕ КРИТЕРИИ ПРОВЕРКИ ГИПОТЕЗ

ПРИМЕРЫ (для самостоятельного решения).

 

1. Для сравнения точности двух манометров было произведено каждым из них несколько измерений давления в камере промышленной установки. По результатам 36 независимых
измерений первым манометром были получены оценки 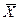₁ = 15,43 и s² = 0,2. Результаты 25 независимых измерений
вторым манометром дали оценки 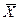₂ = 15,30 и s² = 0,15. При уровне значимости а = 0,05 можно ли расхождение в средних арифметических объяснить случайными ошибками измерений или это расхождение говорит о разной юстировке приборов?

2. Произведены независимые наблюдения над случайны­ми величинами, имеющими нормальные законы распределе­ния с одинаковыми дисперсиями, равными 0,16. Наблюдения
над первой величиной дали результаты: Х₁ = 15,3; Х₂ = 14,8; Х₃ = 15,1; Х₄ = 15,1; Х₅ = 15,2; Х₆ = 15,1;Х₇ = 15,0; X₈ = 15,2; Х₉ = 15,1. У второй случайной
величины реализовались значения: Y₁ = 15,2: Y₂ = 15,0;У₃ = 15,4; У₄ = 15,2; У₅ = 15,3; У₆ = 15,1; У₇ = 15,2;Y₈ = 15,6; У₉= 15,3. При уровне значимости а = 0.05 мож­но ли считать, что наблюдаемые случайные величины имеют
разные математические ожидания?

3. Каждый из двух стрелков произвел по 100 выстрелов по летающим тарелочкам. Первый стрелок попал 56 раз, вто­рой — 44 раза. При уровне значимости а = 0,1 можно ли
считать, что стрелки одинаково меткие?

4. Два пресса штампуют детали одного наименования. Из 1000 деталей, изготовленных первым прессом, 92 оказались низкого качества. Из 600 деталей, изготовленных вторым прес­сом, низкое качество имели 49. При уровне значимости = 0,05 можно ли считать, что доля низкокачественных дета­лей в продукции этих прессов одинакова?