t-критерий Стьюдента.

t-критерий Стьюдента используют для сравнительной оценки средних величин независимых выборок. Закон t-распределения служит основой теории малой выборки, которая характеризует распределение выборочных средних в нормально распределяющейся совокупности в зависимости от объема выборки. t-распределение зависит только от числа степеней свободы k=n–1, причем с увеличением объема выборки n t-распределение быстро приближается к нормальному и уже при n≥30 не отличается от него. Для равночисленных выборок, где n₁=n₂, t-критерий вычисляют по формуле:

 

(6) ,

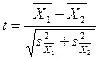где 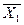, 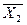- средние арифметические двух независимых выборок,

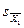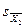, - ошибки средних арифметических.

 

Выражается в сигмах.

Для оценки значения t-критерия используют доверительные вероятности и соответствующие им уровни значимости (см. пункт 6). Согласно нулевой гипотезе, 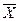₁= 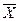₂ (а следовательно, и для генеральной совокупности). Нулевую гипотезу отвергают, если фактически установленная величина t-критерия (t_ф) превзойдет или окажется равной критическому (стандартному) значению t_st этой величины для принятого уровня значимости и числа степени свободы k=n₁+n₂–2. Значение t_st определяют по таблице (таб. 1).

Неопровержение нулевой гипотезы нельзя рассматривать как доказательство равенства между неизвестными параметрами совокупностей, из которых извлечены сравниваемые выборки. В таких случаях вопрос в преимуществе оной статистической совокупности перед другой остается открытым. Ведь не исключено, что при повторных испытаниях нулевая гипотеза может оказаться несостоятельной. Более того, и в тех случаях, когда нулевая гипотеза опровергается, не следует спешить с окончательным выводом.