Проверка гипотезы о нормальности распределения (2)
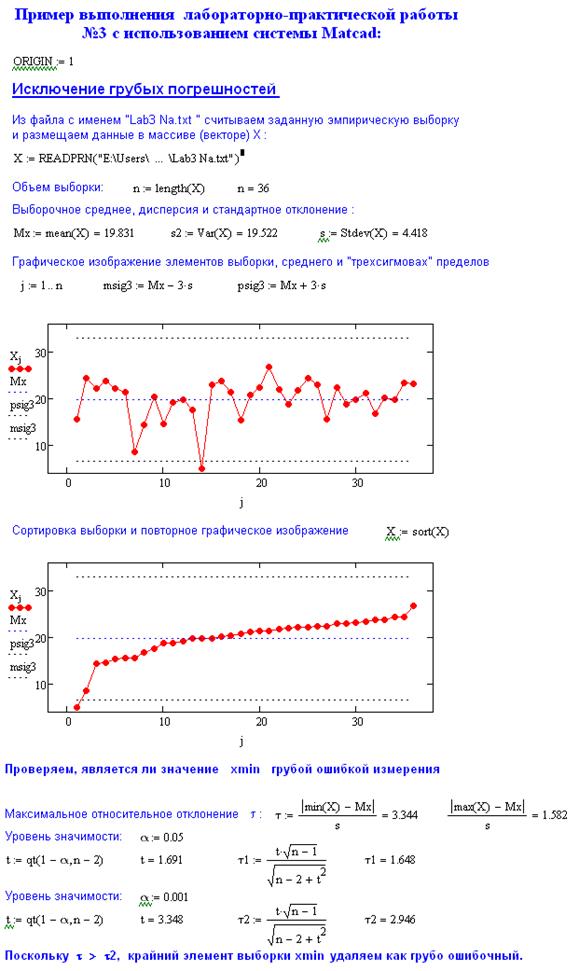
1. Вычислите оценки эмпирического среднего, дисперсии и стандартного отклонения.
2. Вычислите максимальное и минимальное значения выборки.
3. Присвойте конкретное значение числу интервалов разбиения 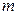 (при выборе числа
(при выборе числа 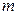 можно пользоваться рекомендациями, приведенными в первой лаб. работе) и вычислите границы интервалов
можно пользоваться рекомендациями, приведенными в первой лаб. работе) и вычислите границы интервалов 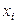 ,
, 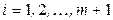 ; крайним границам присвойте значения
; крайним границам присвойте значения 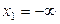 ,
, 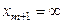 .
.
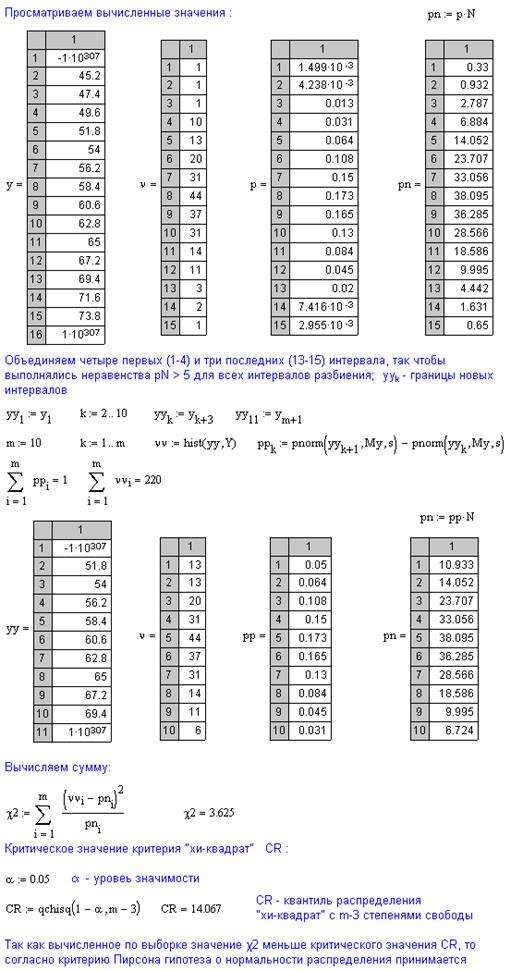
4. С помощью функции hist(x,X) вычислите частоты попадания выборочных значений в интервалы разбиения, а с помощью функции нормального распределения pnorm(x,MX,σ) – теоретические вероятности.
5. Проверьте выполнение условия  и объедините интервалы так, чтобы это условие было выполнено для всех интервалов.
и объедините интервалы так, чтобы это условие было выполнено для всех интервалов.
6. Вычислите сумму (5).
7. Задайте определенный уровень значимости 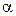 и вычислите критическое значение критерия
и вычислите критическое значение критерия  , т.е. квантиль распределения «хи-квадрат» уровня
, т.е. квантиль распределения «хи-квадрат» уровня  с
с 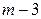 степенями свободы.
степенями свободы.
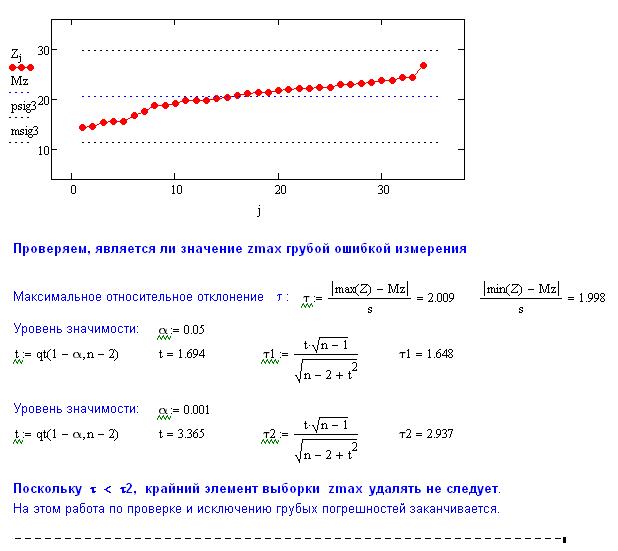
8. На основе неравенства (6) сделайте вывод о принятии или отклонении гипотезы о нормальности распределения.
9. Сделайте выводы по проделанной работе.
10. Сохраните рабочий документ.