ДВУХКОМПОНЕНТНЫЕ ВЕРОЯТНОСТНЫЕ РАСЧЕТЫ ДЕТАЛИ МАШИН.

При двухкомпонентных вероятностных расчетах учитывается рассеивание двух наиболее существенных характеристик несущей способности деталей машин, например рассеивание предельных напряжений, характеризующих прочность материала и рассеивание действующих напряжении, характеризующих нагруженность детали.

Обозначим значения этих характеристик соответственно через x и y. Поскольку x и y являются случайными величинами, то сочетания их различных значений также является случайными величинами. Если наибольшие и наименьшие значения каждой из случайных величин x и y маловероятны, то, очевидно, что тем более маловероятны их сочетания.

Двухкомпонентная схема является основной схемой вероятностных расчетов деталей машин, так как в ней воплощена в вероятностном аспекте основная задача расчетов на прочность, заключающаяся в обеспечении превышения предельных напряжений, характеризующих прочность, над напряжениями, характеризующими нагруженность деталей. При двухкомпонентных расчетах деталей машин оценивается вероятность разности двух независимых случайных величин z = x - y где x - предельные напряжения, характеризующие прочность, а y- напряжения, характеризующие нагруженность деталей. Условием прочности является z>о. Если функциональная зависимость между x и y линейна, то совместная плотность распределения независимых случайных величин x и y, т. е. плотность распределения f(z), может быть определена как композиция плотностей f(x), и f(y), осуществляемая сверткой (складкой) функцией f(x), и f(y). (К свертке прибегают только в том случае, когда формула композиции законов распределения заранее неизвестна и, следовательно, не может быть определена искомая вероятность. )

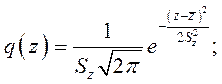Двухкомпонентные вероятностные расчеты деталей машин основаны на законах нормального распределения. Известно, что композиция нормальных законов является также нормальным законом распределения и если z = x - y, то плотность вероятности со средним значением 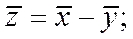и средним квадратическим отклонением 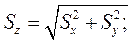На рис. изображена графическая интерпретация двухкомпонентного вероятностного расчета.

а вероятность выполнения этого условия равна площади под кривой распределения, расположенной в правой части, где z ³ 0, то

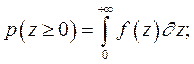и при нормальном законе распределения

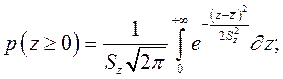Если для удобства вычислений пронормировать распределение вводя обозначение

и учесть, что при Z =0 нижний предел интегрирования (15). а при z ®+¥ верхний предел u ®+¥ , то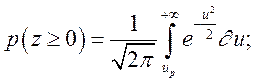

Из этой зависимости видно, что значение p(z ³ 0) При одном и том же u_p всегда одно и то же, и, следовательно, u_p - квантиль нормального распределения. По значениям квантилей, оцениваемых в зависимости от коэффициентов запаса прочности и коэффициентов вариации, определяют вероятность безотказной работы или по значениям коэффициентов вариации и квантилей, соответствующих заданным вероятностям, определяют коэффициент запаса прочности.

Расчетные формулы получают следующим образом [ 6 ]. Если разделить числитель и знаменатель в правой части зависимости (15) на и учесть, что коэффициент запаса прочности и коэффициенты вариации, определенные по средним значениям характеристик прочности и нагруженности , равны соответственно

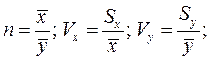то 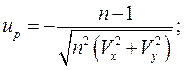(16) или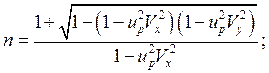 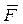Коэффициенты вариации нагруженности деталей машин могут быть определены, в предположении подчинения отклонений нагрузок от заданного режима нормальному закону распределения, следующим образом. Поскольку наибольшие F_мах нагрузки могут быть представлены через средние (номинальные) при помощи “правила трех сигм" как 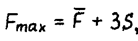то из частного от деления F_maх на F, представляющего собой коэффициент перегрузки, следует

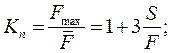откуда поскольку то

Значения коэффициентов перегрузки могут быть найдены по перегрузочным характеристикам двигателей или предохранительных муфт. При определении коэффициентов вариации действующих напряжении следует учитывать характер зависимости напряжений от нагрузок.