Авторегрессионные модели

Рассмотрим класс авторегрессионных моделей, сокращенно обозначаемых АР(р) -модели (число в скобках указывает порядок авторегрессии) или, как принято в специальной англоязычной литературе и мировой статистической практике, AR(p) - models (AutoRegressive processes of order р).

В авторегрессии каждое значение ряда находится в линейной зависимости от предыдущих значений. Если анализируемый динамический процесс зависит от значений, отстоящих до р временных лагов назад, то это авторегрессионный процесс порядка, т.е. AR(р):

y_t=a₁ y_t-1 + a₂ y_t-2 +_…+ a_py_{t-p +} e_t

или

(1 - a₁B + a₂B ²+_…+ a_pB ^p) y_t = Ф(В) y_t = e_t (3.1)

где В — оператор сдвига, т.е. преобразование ряда, смещающее его на один временной такт; Ф(В) — оператор авторегресии.

При этом для выполнения условия стационарности все корни многочлена Ф(В) должны лежать вне единичного круга, т.е. все корни соответствующего характеристического уравнения должны быть по модулю больше 1 и различны.

Рассмотрим простейший вариант линейного авторегрессионного процесса — модель авторегрессии 1-го порядка — AR(1), или марковский процесс.

Эта модель может быть представлена в виде:

y_t = a y_t-1 + e_t (3.2)

где a — числовой коэффициент, |a | < 1, e_t — последовательность случайных величин, образующих “белый шум”.

Основные свойства марковского процесса:

1. M(y_t) = 0;

2. D(y_t) = / (1 - a²);

3. Cov(y_t, y_t±t) = a^t D(y_t);

4. r(y_t, y_t±t) = r(t) = a^t .

Представим y_t = a y_t-1 + e_t в виде:

y_t = a (a y_t-2 + e_t-1) + e_t = a²y_t-2+a e_t-1+ e_t =a²(ay_t-3+ e_t-2) +

+a e_t-1+ e_t =a³ y_t-3 + a²y_t-2+a e_t-1+ e_t = … =

e_t+a e_t-1+ a²y_t-2+… = ; (3.3)

Очевидно, что y_t зависит от всех предыдущих, но не от будущих случайных величин e_t . Отсюда c учетом характера “белого шума”. непосредственно следует, что М(у_t)= 0.

Также получим выражение для дисперсии марковского процесса AR(1), с помощью выражения (3.3):

D(y_t) = (1 + a² + a⁴ + …) = /(1 - a²). (3.4)

Сумма бесконечной геометрической прогрессии записана при условии |a | < 1. Отсюда видно, что при значении a близком к ± 1 дисперсия ряда будет намного больше — дисперсии белого шума. Следовательно, если последовательные значения ряда сильно коррелированны, то даже незначительные возмущения будут порождать размашистые колебания.

Чтобы показать свойства 3 и 4, умножим обе части уравнения (3.2) на y_t-1 и возьмем математическое ожидание:

M(y_t y_t-1) = aM(y_t-1 y_t-1) + M(e_t) M(y_t-1)

где второе слагаемое M(e_t y_t-1) записано с учетом некоррелируемости значений ряда с любыми будущими случайными величинами e_t. Окончательная запись этого соотношения

Сov(y_t, y_t-1) = aD(y_t).

Таким образом,

a = Сov(y_t, y_t-1)/ D (y_t),

т.е. a — коэффициент автокорреляции первого порядка (определяет значение коэффициента парной корреляции между соседними уровнями ряда):

r(1) = a.

Можно показать, что

Сov(y_t, y_t±t) = a^t D(y_t)

а, следовательно,

r(y_t, y_t±t) = a^t = r(t).

Поэтому степень тесноты корреляционной связи между членами последовательности экспоненциально убывает по мере их взаимного удаления друг от друга во времени.

Все автокорреляции марковского процесса можно выразить через автокорреляцию первого порядка:

r(t) = r(1) r(t - 1) = r(1)²r(t - 2) = ... = r(1)^t = a^t.

Значения частной автокорреляционной функции равны нулю для всех лагов k > 2, что может быть использовано при подборе модели. Этот результат верен для теоретической частной автокорреляционной функции и может не выполняться для выборочной автокорреляционной функции. Однако, если выборочные частные корреляции статистически незначимо отличаются от нуля при k > 2, то использование модели AR(1) не противоречит исходным данным.

Условие стационарности ряда для AR(1) определяется требованием к коэффициенту а: |a | < 1 или, что то же самое, корень z₀ уравнения 1- az = 0, являющегося частным случаем характеристического уравнения для общего линейного процесса авторегрессии, должен быть по абсолютной величине больше 1.

Процесс с параметром |a| > 1 является нестационарным. Такие ряды маловероятны в реальных финансово-экономических задачах, так как это подразумевает взрывные ряды, а давление экономической среды не позволяет показателям принимать бесконечно большие значения.

Из авторегрессионных процессов выше первого порядка в экономической практике часто встречаются так называемые процессы Юла. Они описываются с помощью модели AR(2):

y_t = a₁ y_t-1 + a₂ y_t-2 + e_t (3.5)

Определим выражение для вычисления значений автокорреляционной функции r(t), сокращенно АКФ, для любого значения сдвига ряда t . Для этого опять умножим обе части уравнения (3.5) на у_t-t :

y_t у_t-t = a₁ y_t-1 у_t-t + a₂ y_t-2 у_t-t + e_t у_t-t (3.6)

и возьмем математическое ожидание:

M(y_t у_t-t) = g(t) = a₁g(t-1) + a₂ g(t-2). (3.7)

Очевидно, что M(e_t у_t-t ) = 0,так как y _t-k зависит от e_t-t и предшествующих значений, а не от будущих значений e_t,. Разделим обе части равенства (3.7) на g(0):

r(t) = a₁r (t-1) + a₂ r (t-2). (3.8)

Это выражение позволяет вычислить значение АКФ для различных значений лагов t. Подставим последовательно в (3. 8) значение t = 1 и t = 2.

С учетом того, что r(0) = 1, а r(-1) = r(1), получим

r(1) = a₁+a₂ r(1);

r(2) = a₁ r(1) + a₂. (3.9)

Эта система называется системой Юла—Уокера (Yule— Walker) для AR(2).

Если разрешить эту систему относительно a₁ и a₂ ,то получим выражения:

a₁ = r(1)[1 - r(2)]/ [1 - r²(1)];

a₂ = [r(2) - r²(1)]/ [1 - r²(1)]. (3.10)

Выразим из системы (3.9) два первых значения АКФ:

r(1) = a₁/(1- a₂);

r(2) = a₂ + a₁² /(1 - a₂). (3.11)

Определив r(1) и r(2), можно вычислить любые последующие значения АКФ с помощью (3.8).

Получим соотношение, связывающее между собой дисперсию ряда y_t и дисперсию белого шума e_t,равную . Для этого умножим уравнение AR(2) на у_t:

y_t у_t = a₁ y_t-1 у_t + a₂ y_t-2 у_t + e_t ( a₁ y_t-1 + a₂ y_t-2 + e_t )

Возьмем математическое ожидание:

g(0) = a₁ g(l) +a₂ g(2) + .

Очевидно, что М(e_t y_t-1 ) = 0, М(e_t y_t-2 ) = 0, так как у_t не зависит от будущих значений e_t.

Следовательно,

= g(0) -a₁ g(l) -a₂ g(2).

От коэффициентов автоковариации перейдем к автокорреляционным коэффициентам, умножив и разделив правую часть уравнения на g(0):

= g(0) [ 1-a₁ g(l) -a₂ g(2)]. (3.12)

Подставим в него выражения (3.11) для r(1) и r(2) через a₁ и a₂:

g(0) = .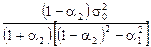

Отсюда, учитывая, что дисперсия должна быть положительна, получаем условия стационарности процесса AR(2). Условия стационарности ряда у, также могут быть получены с учетом (6.14) из требований

| r(1)| < 1, |r(2)| < 1.

Отметим, что те же самые условия получаются из требования, чтобы все корни соответствующего характеристического уравнения 1 - a₁z - a₂z² = 0 лежали вне единичного круга.

Условия стационарности процесса AR(2) могут быть записаны в виде

| a₂| < 1;

a₁ + a₂ < 1;

a₂ ‑ a₁ < 1. (3.13)

ЧАКФ для процесса AR(р) будет иметь ненулевые значения лишь при k £ р, а начиная с лага k = р + 1 теоретическая ЧАКФ равна нулю. Это свойство становится ключевым при подборе порядка р авторегрессионной модели для конкретных экономических временных рядов.

Рассмотренные свойства авторегрессионных моделей и изучение АКФ (ACF) и ЧАКФ (PACF) позволяют сформулировать следующие практические рекомендации по их идентификации:

1. У моделей AR(p) значения коэффициентов АКФ экспоненциально затухают (либо монотонно, либо попеременно меняя знак).

2. ЧАКФ для модели AR(p) имеет выбросы (пики) на первых) лагах, а значения коэффициентов для лагов, больших порядка авторегрессии, статистически незначимы.