Тест Бреуша—Годфри
Тест основан на следующей идее: если имеется корреляция между соседними наблюдениями, то естественно ожидать, что в уравнении (1):


(где  — остатки регрессии, полученные обычным методом наименьших квадратов), коэффициент
— остатки регрессии, полученные обычным методом наименьших квадратов), коэффициент  окажется значимо отличающимся от нуля.
окажется значимо отличающимся от нуля.
Напомним, что уравнение (1) является авторегрессионным уравнением первого порядка.
Практическое применение теста заключается в оценивании методом наименьших квадратов регрессии (1) (напомним, что временной ряд 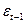 представляет ряд
представляет ряд  со сдвигом по времени на единицу).
со сдвигом по времени на единицу).
Преимущество теста Бреуша—Годфри по сравнению с тестом Дарбина—Уотсона заключается в первую очередь в том, что он проверяется с помощью статистического критерия, между тем как тест Дарбина—Уотсона содержит зону не определенности для значений статистики d. Другим преимуществом теста является возможность обобщения: в число регрессоров могут быть включены не только остатки с лагом 1, но и с лагом 2, 3 и т д., что позволяет выявить корреляцию не только между соседними, но и между более отдаленными наблюдениями. [5]