Графическое диагностирование автокорреляции. Тест серий

После того, как мы обсудили последствия автокорреляции, очевидно, что появляется следующий вопрос — как мы можем обнаружить и исправить ее? Об этом мы поговорим позднее, а сейчас рассмотрим конкретный пример.

В таблице 1 приведены данные по индексам реальной заработной платы за час (Y) и почасовой производительностью (X) в бизнес-секторе американской экономики за период 1959-1998. За базу индексов взят 1992 год, где значение показателей равно 100.

Табл. 1. Индексы реальной заработной платы за час и почасовая

производительность в час, США, 1959-1998 годы

Год	Y	X	Год	Y	X
	58,5	47,2		90,0	79,7
	59,9	48,0		89,7	79,8
	61,7	49,8		89,8	81,4
	63,9	52,1		91,1	81,2
	65,3	54,1		91,2	84,0
	67,8	54,6		91,5	86,4
	69,3	58,6		92,8	88,1
	71,8	61,0		95,9	90,7
	73,7	62,3		96,3	91,3
	76,5	64,5		97,3	92,4
	77,6	64,8		95,8	93,3
	79,0	66,2		96,4	94,5
	80,5	68,8		97,4	95,9
	82,9	71,0		100,0	100,0
	84,7	73,1		99,9	100,1
	83,7	72,2		99,7	101,4
	84,5	74,8		99,1	102,2
	87,0	77,2		99,6	105,2
	88,1	78,4		101,1	107,5
	89,7	79,5		105,1	110,5

Первоначально рассмотрим графическое представление зависимости Y от X, представленную на рис. 7.

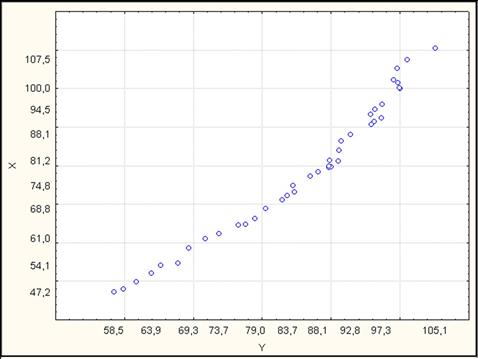
Рис. 7. Индексы реальной заработной платы за час и почасовая производительность в час,

США, 1959-1998 годы

Очевидно, что зависимость данных показателей линейна, поэтому используем классическую модель регрессии для ее описания:

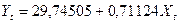
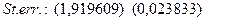
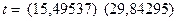
Результаты оценивания параметров регрессии в программе Statistica 6.1 представлены на рис. 8.

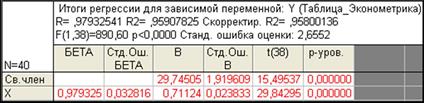
Рис. 8. Результаты оценивания параметров регрессии в программе Statistica 6.1

Насколько надежными являются результаты регрессии, приведенные выше, подвержены ли они действию автокорреляции? Как указывалось ранее, если автокорреляция присутствует, то стандартные ошибки оценки являются заниженными, в результате чего рассчитанные t-статистики ненадежны. Поэтому нам необходимо выяснить, «страдают» ли наши данные от автокорреляции. Далее мы рассмотрим несколько методов ее обнаружения.

Существуют различные способы изучения остатков. Самый простой из них — графически отобразить их зависимость от времени, как на рис. 9, который отображает остатки регрессии из примера. Значения этих остатков приведены в таблице 2 наряду с некоторыми другими данными. [1]

Табл. 2. Значения остатков регрессии, рассчитанные

с помощью программы Statistica 6.1

Год	Наблюд. знач.	Предск. знач.	Остатки	Станд. остатки	Год	Наблюд. знач.	Предск. знач.	Остатки	Станд. остатки
	58,5000	63,3156	-4,81561	-1,81364		90,0000	86,4309	3,56908	1,34418
	59,9000	63,8846	-3,98460	-1,50067		89,7000	86,5020	3,19795	1,20441
	61,7000	65,1648	-3,46483	-1,30492		89,8000	87,6400	2,15997	0,81348
	63,9000	66,8007	-2,90068	-1,09245		91,1000	87,4978	3,60222	1,35666
	65,3000	68,2232	-2,92316	-1,10091		91,2000	89,4893	1,71074	0,64429
	67,8000	68,5788	-0,77878	-0,29330		91,5000	91,1962	0,30376	0,11440
	69,3000	71,4237	-2,12374	-0,79984		92,8000	92,4053	0,39466	0,14864
	71,8000	73,1307	-1,33072	-0,50117		95,9000	94,2546	1,64543	0,61970
	73,7000	74,0553	-0,35534	-0,13383		96,3000	94,6813	1,61869	0,60963
	76,5000	75,6201	0,87994	0,33140		97,3000	95,4637	1,83633	0,69159
	77,6000	75,8334	1,76656	0,66532		95,8000	96,1038	-0,30379	-0,11441
	79,0000	76,8292	2,17083	0,81757		96,4000	96,9573	-0,55728	-0,20988
	80,5000	78,6784	1,82160	0,68605		97,4000	97,9530	-0,55302	-0,20828
	82,9000	80,2431	2,65688	1,00063		100,0000	100,8691	-0,86910	-0,32732
	84,7000	81,7367	2,96326	1,11602		99,9000	100,9402	-1,04023	-0,39177
	83,7000	81,0966	2,60338	0,98048		99,7000	101,8648	-2,16484	-0,81532
	84,5000	82,9458	1,55416	0,58532		99,1000	102,4338	-3,33383	-1,25558
	87,0000	84,6528	2,34718	0,88399		99,6000	104,5676	-4,96755	-1,87087
	88,1000	85,5063	2,59369	0,97683		101,1000	106,2034	-5,10341	-1,92204
	89,7000	86,2887	3,41132	1,28477		105,1000	108,3371	-3,23713	-1,21916

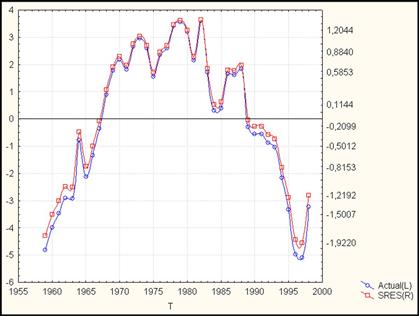
Рис 9. График изменения остатков и стандартизированных остатков

для регрессии примера