МНОЖЕСТВО ПРЕДСТАВИТЕЛЕЙ

 

Условие: Заданы набор С подмножеств конечного множества S и положительное целое число K ≤ |S|.

 

Вопрос: Существует ли такое подмножество S' Í S, что |S'| ≤ К и S' содержит по крайней мере один элемент каждого подмножества из С?

Источник: К этой задаче сводится ВЕРШИННОЕ ПО­КРЫТИЕ.

 

 

2. ДОКАЗАТЕЛЬСТВО ПРИНАДЛЕЖНОСТИ ЗАДАЧИ

К NP-КЛАССУ

 

Структура догадки: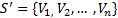

 

1) Проверка размера, где S’ – счетчик элементов, затем сравнение с К.

 

Число шагов равно |S'|+1

 

2) Проверка существования, т.е. наличия всех элементов S' в S.

 

Число шагов равно |S'|*|S|

 

3) Проверка на тавтологию, т.е. на неповторение элементов. Первый элемент сравнивается с n-м элементом, второй элемент сравнивается с n-1 элементом и т.д.

Сумма шагов на данном этапе является суммой арифметической прогрессии.

 

 

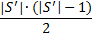
4) Каждое подмножество С не может содержать больше элементов чем | S | , таким образом проверка на данном этапе в худшем случае (все подмножества С содержат по |S|)

 

Число шагов равно |S'|*|C|*|S|

 

5) Итого, сумма всех шагов:

 

S’< S , |S'|+1 + |S'|*|S| + |S'|*(|S’|-1)/2 + |S'|*|C|*|S|<= O(Length(I))^3

 

| S | + | S |*| S | + |S|*(|S|-1)/2 + |S|*|C|*|S|

 

|C|*|S|^2 + |S|^2 + |S|*(|S|-1)/2 + |S|

 

Сумма всех шагов дает полином третьей степени от длины кода задачи, следовательно, задача МНОЖЕСТВО ПРЕДСТАВИТЕЛЕЙ принадлежит классу NP.

 

 

3. ДОКАЗАТЕЛЬСТВО NP- полноты

 

ВЕРШИННОЕ ПОКРЫТИЕ
УСЛОВИЕ. Заданы граф G = (V, E) и положительное число K.
ВОПРОС. Существует ли подмножество V' Í V, такое, что |V’| ≤ K и для любого ребра e ∊ E имеется такая вершина v ∊ V’, что v ∊ e?

Сведем эту задачу к задаче МНОЖЕСТВО ПРЕДСТАВИТЕЛЕЙ. Множество Е состоит из ребер, т.е. подмножеств мощности 2, в которых элементами являются вершины графа G. Требуется, чтобы все подмножества из набора E, содержали хотя бы одну вершину из V'. Тогда можно переписать вопрос задачи ВЕРШИННОЕ ПОКРЫТИЕ таким образом:

Существует ли подмножество V’ Í V, такое, что |V’| ≤ K и V' содержит, по крайней мере, один элемент каждого подмножества из E.

Очевидно, задача ВЕРШИННОЕ ПОКРЫТИЕ является частным случаем задачи МНОЖЕСТВО ПРЕДСТАВИТЕЛЕЙ, в которой мощности всех подмножеств С заданы равными 2.

Т.к. задача МНОЖЕСТВО ПРЕДСТАВИТЕЛЕЙ принадлежит к классу NP, и к ней сведена NP-полная задача ВЕРШИННОЕ ПОКРЫТИЕ, значит, и МНОЖЕСТВО ПРЕДСТАВИТЕЛЕЙ принадлежит к классу NP-полных задач. ■