Applications of derivatives

1.A.Find the interval where the function 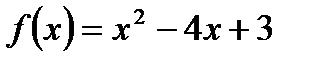is increasing

1.B. Find the interval where the function is increasing.

2.A.If the function has a local minimum at the find

2.B.If the function a local max at the find

3.A.Find the critical points of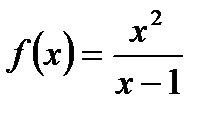

3.B.Find the critical points of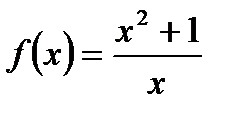

4.A. Find the critical points of the function , and classify each critical point as a local maximum , a local minimum , or neither

4.B. Find the critical points of the function 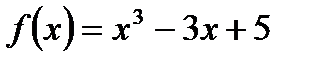, and classify each critical point as a local maximum , a local minimum , or neither.

5.A.Find the absolute exterma of the functi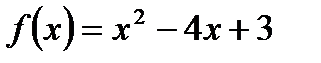on on

5.B.Find the maximum and minimum values of the function on the closed interval

6.A.A man has 40m of fencing that he plans to use enclose a rectangular garden plot. Find the dimensions of the plot that will maximize the area.

6.B.A rectangle has area of 144m . What dimasions will minimize it’s perimeter ?

7.A.Find two positive numbers and such that their sum is 15 and 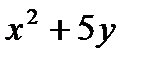is as small as possible.

7.B.If the sum of two positive integers is 10 , then find the minimum value of their squares

8.A.One number is 4 larger than another. How must they be chosen in order to minimize their product

8.B.The product of two real numbers is 150. Find the minimum value of the sum of these two numbers.

9.A.Find the maximum possible area of a right triangle whose hypotenuse is 6cm.

9.B.If the length of hypotenuse of a right triangle is 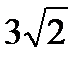the find the maximum values of the area of triangle.

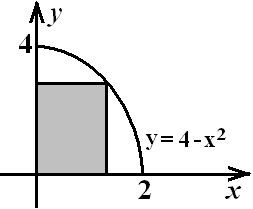
10.A. Find the area of the largest rectangle that has two

vertices on the 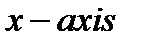and another two nabove the 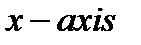on the parabola

 

1. The sum of two numbers is 18, then find the maximum value of the product of the numbers.

2. The sum of two positive numbers is 21, then find the maximum value of the sum of their squares.

3. What is the maximum value of the area of a right triangle whose hypotenuse is ?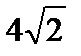

4. What is the maximum value of the area of an isosceles triangle if its perimeter is 18?

5. Find the maximum value of the area of the rectangle ABCD which is inscribed in a circle

with radius R.

(picture 1)

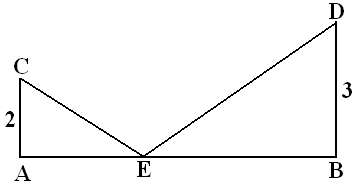
6. In the given figure , and . If E is any point on then find the

minimum length of 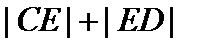. (picture 2)

7. What is the maximum height of a ball if the height of the ball depending on the time is given by the

formula .?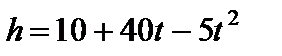

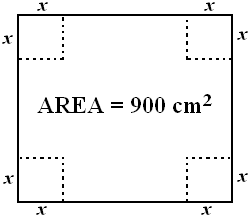
8. A square with an area 900 cm² is used to make a prism by removing the small squares

from each vertex, given as in the figure. If the volume of prism is desired to be maximum,

then find the value of . (Prism does not have upper surface) (picture 3)

9. An isosceles triangle ABC which is inscribed in a circle with radius R has and

. If the perimeter of triangle is desired to be maximum then find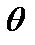

12. What is the height of a cylinder which is inscribed in a sphere if the volume of cylinder is desired

to be maximum? (R is radius of sphere)

13. A cylinder with maximum volume is inscribed in a cone. Find the height of cylinder if the radius and height of cone are r and h respectively?

14. A right cone with a maximum volume is placed in a sphere with 6 cm radius, and then find the volume of the cone.

15. What is the closest point on the parabola 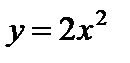to the point ?

 

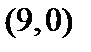Permutation

1.In how many different ways can the flags of 11 countries be arranged in a row?

2.How many different four-digit numbers can be formed from the digits of 0, 2, 4 and 7?

3.Using the digits of 0, 1, 2, 3, 4 and 5, how many

a. three digit odd numbers are there?

b. four digit even numbers are there?

c. three digit odd numbers so that no digit is used more than once are there?

4.How many positive even integers less than 1000 can be formed from digits of 0, 2, 4, 6 and 8?

5.How many three digit numbers can be formed from the digts of 0, 2, 4, 6 and 8? How many of them are greater than 400?

6.How many even numbers between 300 and 600 can be formed from the digits of 2, 3, 4, 5 and 6?

7.How many different 5 letter words can be formed from the letters “G, A, L, A, T, A” ?

8.How many permutations of all the letters in “ULAANBAATAR” end with T ?

9.How many permutations of all the letters in “DARKHAN” begin with the prefix “HA”?

10.2 golden, 3 silver and 6 bronze -identical- coins are distributed among 11 children. Each child receives one coin. In how many ways can the coins be distributed?

11.3 girls and 3 boys are seated around a circular table. In how many ways can they sit alternately?

12.How many permutations of the words “MARMARA” begin with A?

13.In how many ways can 4 Mongolians, 5 Turkish and 2 Russians be seated in round table so that

a. the same nationality must not sit together?

b. one Mongolian and any other nationality must sit alternately?

14.Toss a coin ten times and observe the sequence of heads or tails that results. Answer followings.

a. How many different sequences are possible?

b. How many of the sequences contain four heads?

15.Find the number of ways in which 5 history, 4 geography and 2 psychology books can be placed on a shelf without restriction

a. so that all books of the same branch are together.

b. so that all geography books are together.

c. so that all history books are together.

d. so that the arrangement begins and ends with a psychology book.

16.Show that P(n,r)-P(n, r-1) = (n-r)P(n, r-1)

1.Find the solution set of the followings.

1. ,

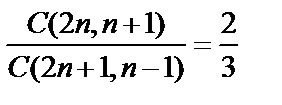2.Let A be a set with 6 elements. Find the number of subsets of A which contains

a. 3 elements.

b. at least 3 elements.

c. less than 4 elements.

3.How many of the 3-person groups chosen from 4 girls and 5 boys contain

a. at least one boy? b. at least two girls?

4.In how many ways can 5-person groups be formed from 12 students so that Batbaatar and Zolchimeg will certainly be in the group?

5.A 5-person group will be chosen among 10 English and 8 German teachers.

a. In how many ways can this be done?

b. How many of these groups has 3 English and 2 German teachers?

c. In how many of these groups the number of German teachers is more than the number of English teachers?

6.An urn contains 9 red and 6 white balls. A sample of 5 balls is to be selected.

a. How many different samples are possible?

b. How many samples contain all red balls?

c. How many samples contain 3 red balls and 2 white balls?

7.In how many ways can 12 different presents be distributed among 4 children, if

a. each child gets 3 presents?

b. a certain child gets 6 and each of the others gets 2 presents?

c. of the children gets 6 and each of the others gets 2 presents?

8.Seven different objects must be distributed among three people. In how many ways can it be done if one or two of them can get no objects?

return false">ссылка скрыта

9.Eleven lines, four of which are parallel to each other, lie in a plane

a. How many intersection points can be obtained at most?

b. Answer "part a" if 5 of these lines pass through the same point A.

10.How many different six-digit numbers are there whose three digits are even and three digits are odd?

11.6 points lie in a plane. No three are collinear. How many intersection points can be obtained from the lines which connect these points?

 

1.If (2x-3y)⁹= …+c.x².y⁷+…+d. x⁷.y²+….. then c+d=?

2.Find the sum of all coefficient of the expansion of (2x-3y)⁸, and find the constant value of expansion.

3.Get all the coefficients in the expansion of (x+ 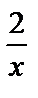)⁷. Then try to see Pascal Triangle Numbers in the expansion.

4.Find the coefficient of the third term of the expansion of .

5.Find n if the constant term of the expansion of is the 5^th term.

6.What is the coefficient of the term including x¹² in expansion of ( 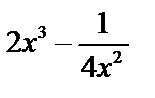)⁹?

7.What is the coefficient of the term including x in expansion of ( )¹³?

8.If the coefficient of the term a² in expansion of (3a-2)ⁿ is 216 then n=?

9.What is the coefficient of the term including x⁵ in expansion of ( )¹⁰?

10.What is the coefficient of the term including x⁴.y⁴.z² in expansion of (x+y+z)¹⁰?