Вычисление цепи методом непосредственного применения законов Кирхгофа
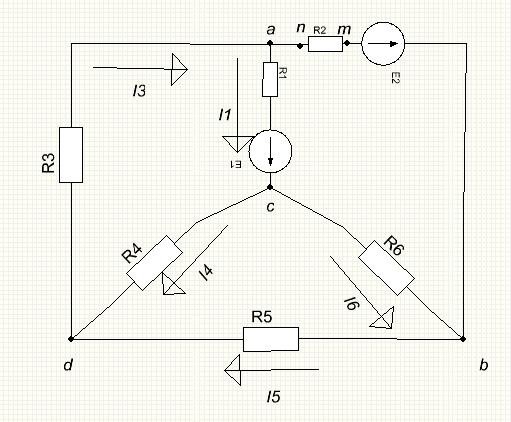
1.1 Определил количество ветвей, узлов и независимых контуров в схеме (рис. 1.2):
b=6,
y=4,
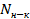 =(b-(y-1)=3
=(b-(y-1)=3
1.2 Произвольно выбрал и указал на схеме (рис 1.2) направления токов в ветвях.
1.3 Составил уравнения в соответствии с I законом Кирхгофа:
узел d:  -
-  -
- 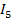 = 0
= 0
узел b:  -
-  +
+ 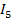 = 0
= 0
узел c:  -
-  -
- 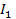 = 0
= 0

Рисунок 1.2
1.4. Выбрал следующие независимые контура (I контур –acd, II контур – acb, III контур – cdb) и принял указанное на схеме (рис. 1.2) направление обхода этих контуров: I и III контуры – против стрелки часов, II контур – по стрелке часов.
1.5. Составил для указанных независимых контуров уравнения в соответствии со II-м законом Кирхгофа:
контур I:  -
- 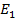 =
=  -
-  -
-  ;
;
контур II:  =
=  +
+  +
+  ;
;
контур III: 0 =  +
+  +
+  ;
;
1.6. Получил следующую систему из линейных уравнений:
 -
-  -
- 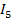 = 0
= 0
 -
-  +
+ 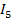 = 0
= 0
 -
-  -
- 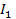 = 0
= 0
3,6 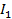 - 39
- 39  - 36
- 36  = -15
= -15
3,6 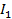 + 30
+ 30 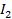 + 36
+ 36  = 3
= 3
39  + 9,7
+ 9,7  + 36
+ 36  = 0
= 0
1.7. Для решения полученной системы линейных уравнений методом Гаусса привёл ее к канонической векторно-матричной форме:

1.8. Решение полученной системы с помощью программы “Расчет сложной цепи постоянного тока” дает результат: значения токов
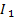 = -0,1353 А,
= -0,1353 А,
 = 0,1679 А,
= 0,1679 А,
 = 0,3032 А,
= 0,3032 А,
 = 0,0922 А,
= 0,0922 А,
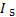 = -0,21099 А,
= -0,21099 А,
 = -0,0431 А.
= -0,0431 А.
1.9. Проверка выполнения баланса отдаваемой и потребляемой мощностей:
 +
+ 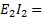
 +
+  +
+ 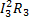
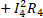 +
+  +
+  ;
;
 = 5,0517 Вт =
= 5,0517 Вт =  = 5,051322 Вт.
= 5,051322 Вт.
1.10. Так как ток 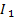
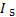
 имеет знак “-”, то изменяю его первоначально принятое направление.
имеет знак “-”, то изменяю его первоначально принятое направление.
1.11. Провёл дополнительно контроль решения, проверив выполнение II закона Кирхгофа во внешнем контуре abd:
 +
+  +
+  =
=  ,
,
5,037+ 2,0466+ 10,9152= 17,9988 ≈18.
2. Расчет тока в цепи источника  (через резистор
(через резистор  ) методом эквивалентного генератора.
) методом эквивалентного генератора.
2.1. Заменим исходную схему (рис. 1.1) схемой эквивалентного генератора (рис. 1.3), где ток находится по формуле согласно закону Ома:
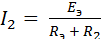 ,
,
Рисунок 1.3
Так как схемы на рис 1.3 эквивалентны, напряжение холостого хода с зажимов будем искать, создав режим холостого хода в исходной схеме между точками m и n (рис. 1.4).
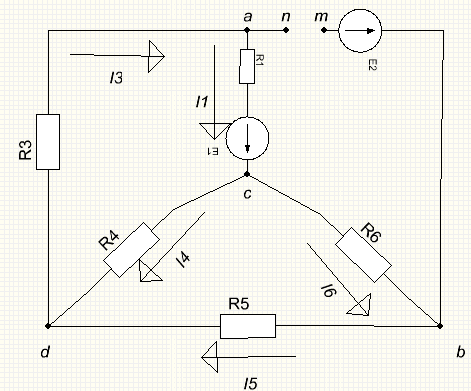
Рисунок 1.4
2.2. Выбрал произвольное направление напряжения холостого хода и токов, определил направления токов в цепи (см. рис 1.4) , как токов в простой цепи, направления которых определяются полярностью источника ЭДС , и составил уравнения в соответствии со ІІ законом Кирхгофа для контура nacbm , обходя его по часовой стрелке, рис 1.4:
 -
- 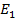 =
=  -
- 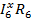 -
-  (1)
(1)
2.3. Для расчета значений 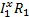 и
и 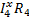 удалил из схемы ветвь ac (в ней отсутствует ток) (рис. 1.5) и произвёл расчет образовавшейся простой цепи методом “свертывания” (рис. 1.6, 1.7, 1.8):
удалил из схемы ветвь ac (в ней отсутствует ток) (рис. 1.5) и произвёл расчет образовавшейся простой цепи методом “свертывания” (рис. 1.6, 1.7, 1.8):

Рисунок 1.5
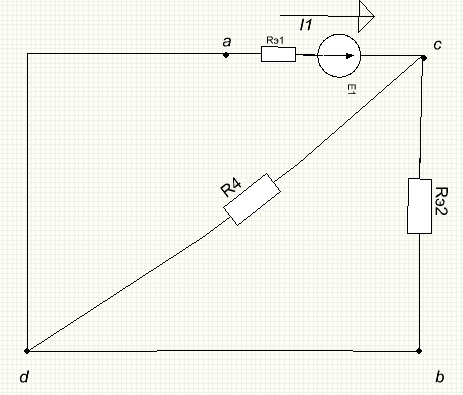
а) прямой ход
Рисунок 1.6
 =
=  +
+ 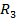 = 39,6 Ом,
= 39,6 Ом,

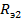 =
= 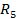 +
+  = 45,7 Ом;
= 45,7 Ом;
Рисунок 1.7
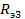 =
= 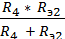 = 21,0425 Ом;
= 21,0425 Ом;

Рисунок 1.8
 =
=  +
+ 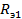 = 60,6425 Ом;
= 60,6425 Ом;
б) обратный ход
 =
= 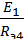 = 0,2473А,
= 0,2473А,
 =
=  *
* 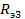 = 5,2049В,
= 5,2049В,
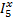 =
= 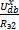 = 0,1139 А.
= 0,1139 А.
2.4.Подставляя значения токов , в уравнение (1), вычисляем значение :
 =
=  -
- 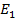 +
+ 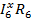 +
+  = 3+ 4,1001 + 0,8903 = 7,9904 В
= 3+ 4,1001 + 0,8903 = 7,9904 В
2.5. Для расчета  заменил в схеме рис. 1.4 источники
заменил в схеме рис. 1.4 источники  и
и 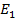 их внутренним сопротивлением, равным нулю, и получил пассивную цепь (рис. 1.9).
их внутренним сопротивлением, равным нулю, и получил пассивную цепь (рис. 1.9).

Рисунок 1.9
2.6. Для “сворачивания” схемы рис. 1.9 и определения значения  заменил “треугольник” сопротивлений
заменил “треугольник” сопротивлений  ,
,  ,
,  эквивалентной “звездой”. В результате получил новую цепь (рис. 1.10), которая может быть “свернута” (рис. 1.11).
эквивалентной “звездой”. В результате получил новую цепь (рис. 1.10), которая может быть “свернута” (рис. 1.11).

Рисунок 1.10
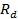 = 4,4664 Ом,
= 4,4664 Ом,
 = 4,1228 Ом,
= 4,1228 Ом,
 = 16,5762 Ом.
= 16,5762 Ом.

Рисунок 1.11
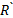 =
= 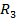 +
+ 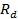 = 40,4664 Ом,
= 40,4664 Ом,
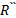 =
=  +
+  = 20,1762 Ом,
= 20,1762 Ом,
 =
=  +
+  =
= 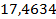 Ом.
Ом.
2.7. Таким образом, исходная цепь при использовании метода эквивалентного генератора для расчета тока через резистор  преобразуется следующим образом (рис. 1.12):
преобразуется следующим образом (рис. 1.12):
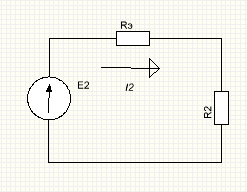
Рисунок 1.12
и, следовательно,
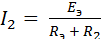 =
=  = 0,1638А.
= 0,1638А.
Направление тока  соответствует направлению напряжения
соответствует направлению напряжения  .
.